Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.3 - Ex. 16
Faça um esboço do gráfico e ache o limite indicado, se existir; se não existir, indique a razão disso.
Lembrando que é definido como
Passo 1
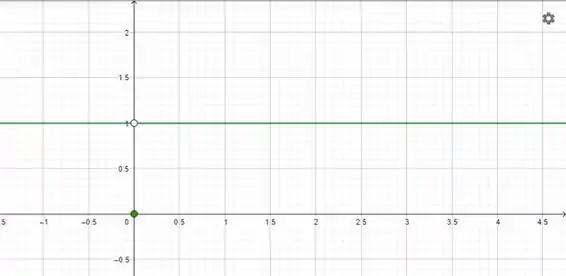
Vamos começar fazendo um esboço de . Para isso temos que entender um pouquinho só como é essa nossa
O enunciado disse que
Pegando a definição dessa função dois , quando passamos o modulo, o que acontece é que tudo que é negativo fica positivo
Então, vai ser
Podemos resumir essa função em
Então nosso gráfico vai ser sempre , menos no , que será o próprio
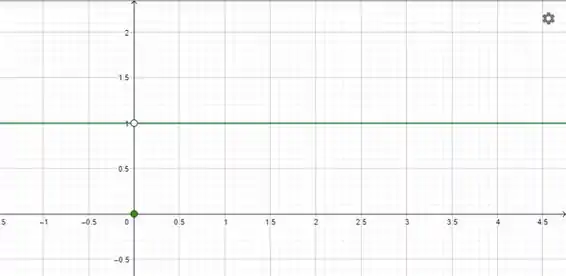
Para indicar aquele que a função não é em devemos colocar aquela bola aberta.
Passo 2
Letra
Agora vamos aos limites que ele pediu
Aqui, temos que ver o comportamento da função quando se aproxima de pela direita. Que é se aproximar de por valores maiores que .
Olhando o gráfico, chegando perto de pela direita, a nossa função se aproxima de .
Mesmo que ela de fato seja em , a reta verdinha chega muuuuuito perto de na verdade.
Passo 3
Letra
Agora o outro
Aqui, temos que ver o comportamento da função quando se aproxima de pela esquerda. Que é se aproximar de por valores menores que .
Olhando o gráfico, chegando perto de pela esquerda, a nossa função se aproxima de .
Mesmo que ela de fato seja em , a reta verdinha chega muuuuuito perto de na verdade.
Passo 4
Letra
Para o limite que ele pediu, temos que comparar os limites laterais.
Se eles forem iguais, o limite em vai existir e será esse valor. Se eles forem diferentes o limite não existe.
Pelas letras e , os dois limites laterais são iguais a , então
Resposta
