Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.3 - Ex. 16
- Faça um esboço do gráfico da função no intervalo indicado;
- Teste as três condições (i), (ii) e (iii) das hipóteses do teorema de Rolle e determine quais entre elas são satisfeitas;
- Se as três condições de (b) forem satisfeitas, determine um ponto no qual existe uma reta tangente horizontal.
Passo 1
Como é a junção de uma função constante com uma modular, é preciso observar o comportamento do módulo em cada intervalo de para poder esboçar o gráfico da função. Vamos atribuir alguns valores para e observar o comportamento de .
Seentão e:
Seentão e:
Seentão e:
Seentão e:
Seentão e:
Fazendo o esboço de no intervalo temos:
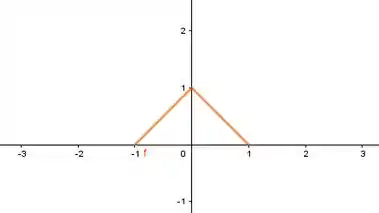
Passo 2
Observe que se temos , que é uma função polinomial. Logo é contínua em . E se , temos , que é uma função polinomial. Logo é contínua em . Precisamos verificar sua continuidade quando . Assim:
Como , temos que é contínua em . Portanto, a função é contínua em .
Como e são funções polinomiais, então é derivável em e . Precisamos verificar quando . Assim, da definição de derivada:
E também:
Como , temos que não é derivável em . Portanto, não é derivável em .
Observe que .
Resposta
Portanto, só satisfaz duas das três condições do teorema de Rolle, logo não é possível aplicá-lo.