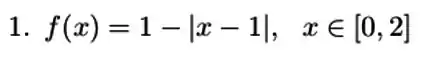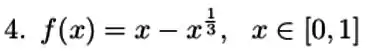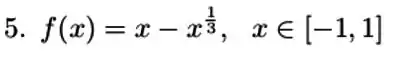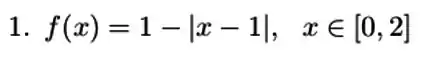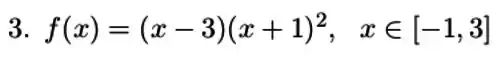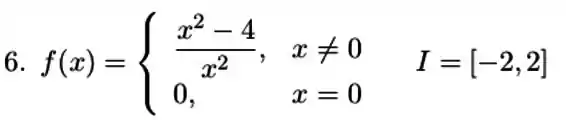Exercícios de Teorema de Rolle e Valor Médio - Lista de Exercícios Resolvida

A função abaixo satisfaz as hipóteses do teorema do valor médio no intervalo dado? Justifique sua resposta.

A função abaixo satisfaz as hipóteses do teorema do valor médio no intervalo dado? Justifique sua resposta.

A função:

é zero quando e e derivável em, mas sua derivada em nunca é zero. Explique por quê. O teorema de Rolle não diz que a derivada deveria ser zero em algum lugar em ? Justifique sua resposta.

13. Se , então .

Essa afirmação é verdadeira ou falsa?

Seja. Mostre que , mas não existe um número em tal que . Por que isso não contradiz o Teorema de Rolle?

Em cada um dos itens abaixo, verifique que a função satisfaz as três condições do Teorema de Rolle no intervalo indicado. Em seguida, encontre todos os números que satisfazem a conclusão do Teorema.

12) Seja uma função polinomial não constante.

a) Prove que, entre dois zeros consecutivos de (isto é, dois valores de que anulam a derivada e tal que entre eles não existe outro valor que anula a derivada), existe no máximo uma raiz de .

Nos exercícios de a , verifique se o teorema de Rolle pode ser aplicado à nos intervalos indicados

.

Verifique se a função satisfaz as hipóteses do teorema do valor médio no intervalo dado. Então, encontre todos os números c que satisfaçam a conclusão do teorema do valor médio.

com domínio

Em cada um dos itens abaixo, verifique que a função satisfaz as três condições do Teorema de Rolle no intervalo indicado. Em seguida, encontre todos os números que satisfazem a conclusão do Teorema.

Verifique se a função satisfaz as hipóteses do Teorema do Valor Médio no intervalo dado. Então, encontre todos os números que satisfaçam a conclusão do Teorema do Valor Médio:

Sejam e números reais tais que:

Mostre que o polinômio possui ao menos uma raíz no intervalo .

Dica: Use o polinômio:

Seja contínua em , diferenciável em , com e . Prove que existe um ponto no gráfico de em que a reta tangente é paralela à reta .

Mostre que admite uma única raiz no intervalo .

Mostre que, se e , então a equação tem exatamente uma raiz real.

ME03) Seja uma função contínua no intervalo e derivável em , que assume os valores , , e . Considere as afirmações:

1. A equação tem pelo menos uma solução no intervalo
2. A equação tem exatamente uma solução no intervalo
3. A função admite um ponto crítico no intervalo

Pode-se dizer com certeza que:

1. Todas as afirmações são falsas
2. Somente as afirmações e são verdadeiras
3. Somente as afirmações e são verdadeiras
4. Todas as afirmações são verdadeiras
5. Somente a afirmação é verdadeira

Se então:

Se então:

Se então:

Se então:

Se então:

Suponha que para todos os valores de . Mostre que

Verifique se a função satisfaz as hipóteses do teorema do valor médio no intervalo dado. Então, encontre todos os números c que satisfaçam a conclusão do teorema do valor médio.

com domínio

Verifique se a função satisfaz as hipóteses do teorema do valor médio no intervalo dado. Então, encontre todos os números c que satisfaçam a conclusão do teorema do valor médio.

com domínio

Seja. Mostre que , mas não existe um número em tal que . Por que isso não contradiz o Teorema de Rolle?

Considere as afirmações a seguir

Seja uma função diferencial em tal que e . Então existe tal que ;

Seja uma função diferencial em e suponha que existe tal que . Então ;

Sejam e funções diferenciáveis em tais que para todo e suponha, além disso, que . Então .

Podemos concluir com certeza que:

: Todas as afirmações são verdadeiras.

: Apenas a afirmação é verdadeira.

: Apenas as afirmações e são verdadeiras.

: Apenas as afirmações e são verdadeiras.

: Apenas as afirmações e são verdadeiras.

Enuncie corretamente o Teorema do Valor Médio e descreva graficamente o seu significado geométrico.

Seja derivável em . Suponha que . Prove que existe um ponto no intervalo tal que .

Dica: Use uma função auxiliar

ME01) Sejam dada por e cuja existência é garantida pelo Teorema do Valor Médio para no intervalo . O valor de é:

ME01) Considere uma função derivável com e , e considere as afirmações abaixo:

1. possui pelo menos uma raíz
2. Para algum , vale que
3. Para algum , vale que

Escolha a alternativa correta:

1. Somente é verdadeira
2. Somente é verdadeira
3. Somente é verdadeira
4. e são verdadeiras
5. e são verdadeiras
6. Todas são verdadeiras
7. Todas são falsas

Use o Teorema do Valor Médio para demonstrar a desigualdade

para todo e

Use o Teorema do Valor Médio para demonstrar a desigualdade

para todo e

Encontre todos os números que satisfaçam à conclusão do Teorema do Valor Médio nos seguintes casos:

b)

Encontre todos os números que satisfaçam à conclusão do Teorema do Valor Médio nos seguintes casos:

c)

Mostre que a equação admite três raízes reais distintas.

Prove que a equação tem exatamente duas raízes reais.

Encontre todos os números que satisfaçam à conclusão do Teorema do Valor Médio nos seguintes casos:

d)

Seja contínua em , diferenciável em , com e . Prove que existe um ponto no gráfico de em que a reta tangente é paralela à reta .

Seja uma função derivável. O gráfico de sua derivada está ilustrado abaixo.

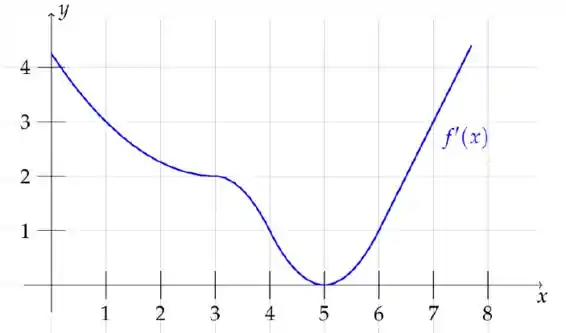
A afirmação que pode não estar correta é:

a)

b)

c)

d)

e)

Supondo que é um intervalo aberto, use o Teorema do Valor Médio para provar as afirmações seguintes:

1. Se para todo então tal que para todo
2. Se para todo . então para todo

Seja . Mostre que não existe um valor de em tal que . Por que isso não contradiz o Teorema do Valor Médio?

Seja . Mostre que não existe um valor c tal que . Por que isso não contradiz o Teorema do Valor Médio?

Existe função tal que e para todo

Em cada um dos itens abaixo, verifique que a função satisfaz as três condições do Teorema de Rolle no intervalo indicado. Em seguida, encontre todos os números que satisfazem a conclusão do Teorema.

Mostre que a equação tem exatamente uma raiz real

Enuncie os Teoremas de Rolle e do Valor Médio.

Seja derivável tal que e para todo . Qual o menor valor possível para ? Justifique.

Mostre que admite uma única raiz no intervalo .

Mostre que a equação tem exatamente uma raiz real

Mostre que a equação tem exatamente uma raiz real

Uso o Teorema do Valor Intermediário junto com o Teorema de Rolle para provar que o polinômio , possui um único zero real (raiz da equação .

Mostrar que a função , , tem exatamente um zero real.

Estude o exemplo 1 página 297 de [ST]. Em seguida, encontre os intervalos nos quais f (x) é crescente ou decrescente nos seguintes casos:

b)

Estude o exemplo 1 página 297 de [ST]. Em seguida, encontre os intervalos nos quais f (x) é crescente ou decrescente nos seguintes casos:

b)

Usando o Teorema do Valor Médio prove as desigualdades

Para quaisquer .

Um empresário verificou que quando vendia liquidificadores a reais cada um, os clientes compravam um total de x = 8000/p liquidificadores por mês. Sabendo que em meses o preço dos liquidificadores será de reais, calcule a taxa de variação da demanda mensal de liquidificadores com relação ao tempo, daqui a 16 meses.

Para que valores de a função

.

satisfaz as hipóteses do TVM no intervalo [0, 2]?

Mostre que a equação tem no máximo duas raízes reais.

Estude o exemplo 1 página 297 de [ST]. Em seguida, encontre os intervalos nos quais f (x) é crescente ou decrescente nos seguintes casos:

Determine o número de raízes reais distintas que o polinômio

possui.

Dica: Use o Teorema do valor médio para mostrar que possui no máximo raízes reais distintas e em seguida o Teorema do Valor Intermediário para garantir a existência delas.