Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.10 - Ex. 14
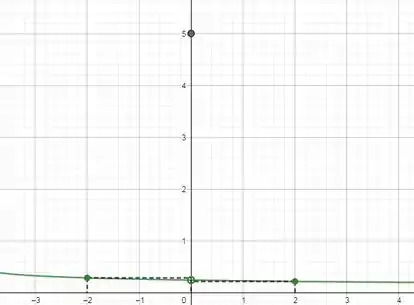
Faça um esboço do gráfico de uma função satisfazendo as hipótese do Teorema 2.10.3 para a qual não é definida. A função está definida no intervalo aberto , exceto em 0. Além disso, seja se e seja igual ao número. Mostre, na figura, que .
Passo 1
Vamos tomar
E que satisfaz a condição de intervalo e por ser uma função racional , ou seja, não está definida em 0.
Passo 2
Agora vamos determinar
Passo 3
Como , então esta função satisfaz todas as condições e nos resta esboçar o gráfico de .
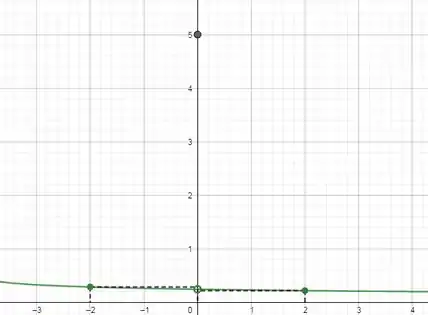
Resposta
Exercícios de Livros Relacionados
Explique porque a função é descontínua no número dado a . Desenho o gráfico da função.
Use o Teorema do Valor Intermediário para mostrar que existe uma raiz da equação dada no intervalo especificado f x = x 3 = 1 - x ,( 0 ,1 )
Use a definição de continuidade e as propriedades dos limites para mostrar que a função é contínua em um dado número a .
Prove, sem usar gráficos, que o gráfico da função tem pelo menos dois pontos interceptando o eixo x no intervalo especificado.
Use a definição de continuidade e propriedades dos limites para demonstrar que a função é contínua em um dado número a . f x = x 2 + 7 - x , em a = 4 .