Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.Revisão - Ex. 17
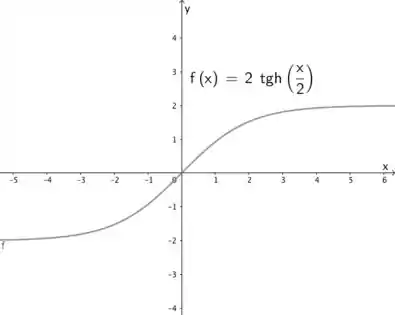
Faça um esboço do gráfico da função
Passo 1
Pessoal, para esboçar o gráfico desta função, nós precisamos ter uma ideia de como é o gráfico da função , e a partir dele nós vamos usar transformações até chegar no gráfico da função pedida. Lembrando que
O gráfico da função apresentado no livro é
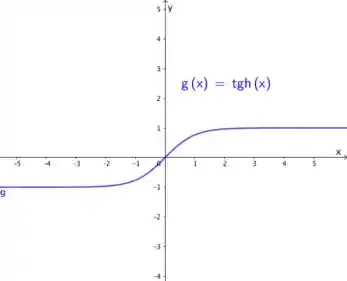
Seu domínio é o conjunto e sua imagem é o intervalo .
Uma característica desse gráfico é que as retas e são duas assíntotas horizontais deste gráfico, ou seja, quando o é infinitamente grande, e quando é infinitamente pequeno, .
Passo 2
A primeira transformação que faremos no gráfico elementar para se tornar o gráfico da é multiplicar por e ficar com . O que isso vai mudar no meu gráfico inicial?
Bom, quando multiplicamos o por uma constante , a interpretação geométrica é um esticamento horizontal da função. O domínio continua e sua imagem continua sendo o intervalo .
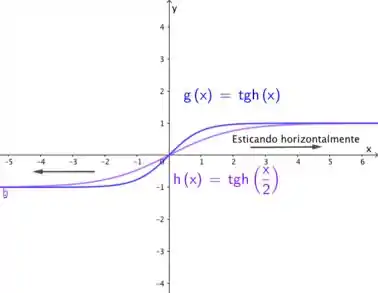
Você pode pensar assim também para entender melhor, para eu ter o valor , que antes eu obtia fazendo em , agora eu preciso ter na nova função que é e isso indica que os pontos da função , no caso do primeiro quadrante, foram puxados para direita, veja que agora preciso de um valor de mais à direita para ter o mesmo valor de (Esticamento horizontal).
Passo 3
Agora devemos perceber que é duas vezes , isso indica que todos os valores de serão multiplicados por dois, o que causa um esticamento vertical da função, como vocês podem perceber abaixo:
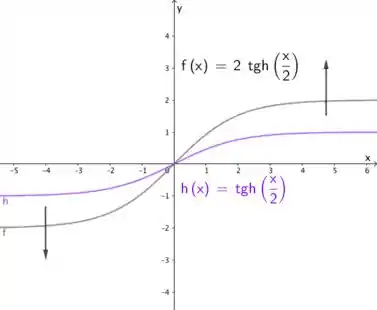
O domínio continua , mas agora sua imagem será intervalo .
O legal aqui é que, como antes as assíntotas horizontais eram e , agora serão e . Elas também sofrem o efeito do esticamento vertical. Bacana, né?
Resposta
