Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 89
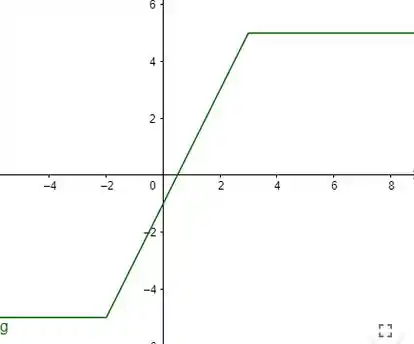
Faça o gráfico da função abaixo, localizando seus valores extremos e onde ocorrem.
Passo 1
Primeiro, abriemos o módulo, para tornar mais simples o processo de derivar a função. Em seguida, igualaremos a 0 para determinar os pontos críticos da função.
Em seguida, faremos o gráfico da função.
Por fim caracterizaremos os pontos, ou intervalos, em máximos e mínimos.
Passo 2
Abrindo o módulo, temos:
Passo 3
Derivando a função acima, temos:
Dessa forma, vemos que a função é constante quando . Portanto analisaremos o interior de , que é quando a função tem um comportamento diferente.
Passo 4
Fazendo ponto a ponto, temos a seguinte tabela:
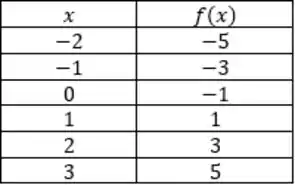
Passo 5
Desenhando o gráfico, vemos que:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 7 e 8, determine os valores máximo e mínimo absolutos de f sobre o intervalo.
a. Dê um exemplo de uma função derivável f cuja primeira derivada seja zero em algum ponto c , embora f não tenha nem um máximo local nem um mínimo local em c . b. Como isso é consistente com o Teorem
Quais são os valores máximo e mínimo da função y = | x | no intervalo - 1 ≤ x1 ? Observe que o intervalo não é fechado.Isso é consistente com o teorema do valor extremo para funções contínuas? Por quê
Nos Exercícios 7 e 8, determine os valores máximo e mínimo absolutos de f sobre o intervalo.
(Continuação do Exercício 13.)b. Mostre que f tem um valor máximo local em x = 5 7 ≈ 1,2585 e um valor mínimo local em x = 2 3 ≈ 1,2599 .