Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 48
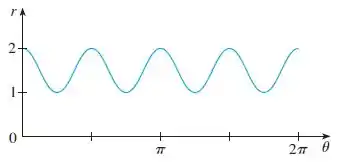
A figura mostra o gráfico de em função de nas coordenadas cartesianas. Use-a para esboçar o gráfico polar correspondente
Passo 1
A questão nos mostra um gráfico representado em coordenadas cartesianas e nos pede para escrever como ficaria esse gráfico em coordenadas polares.
Como sabemos, as coordenadas cartesianas são retangulares, dando valores em eixos perpendiculares entre si.
Nas coordenadas polares, no entanto, temos uma coordenada chamada curvilínea, o que quer dizer que o espaço que ela representa não é retangular.
Os pontos nessas novas coordenadas são dados em termos de um vetor representando o deslocamento radial (na direção do cento) e outro angular (descrevendo a direção entre o eixo e o vetor radial).
Com isso, a questão nos pede para mostrar como esse gráfico está representado em termos das coordenadas polares.
Para resolver, primeiro precisamos escrever a função como função do ângulo . Assim que tivermos isso podemos esboçar nosso gráfico.
Passo 2
Observando o gráfico podemos perceber que essa é uma curva cossenoidal, uma vez que ela atinge seu ponto máximo quando . A amplitude da onda (do vale ao pico) é de uma unidade, mostrando que esse cosseno teve sua amplitude reduzida pela metade. Então, até o momento temos que:
Nesse resultado temos o surgimento de uma constante chamada . Essa constante é o chamado número de onda e é importante para avaliar quantas oscilações há em determinado intervalo.
Vamos analisar o período dessa função. Vemos aqui que a distância entre picos (ou vales) é de .
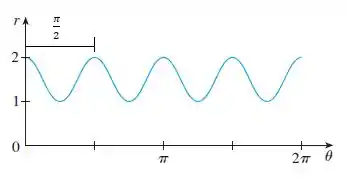
Podemos escrever o período da seguinte forma:
Assim, podemos escrever a equação polar da seguinte maneira:
Passo 3
No passo 1 descobrimos que a amplitude da função era de . No gráfico, a função está oscilando entre , certo? Se com a amplitude em o valor máximo que ela está atingindo é , isso implica em dizer que há um deslocamento vertical da função de unidade para cima. Assim, a equação polar final fica igual a:
As coordenadas que iremos trabalhar possui eixos radiais e eixos em forma de círculo que variam de até .
A função nos mostra o tamanho da distância da origem até algum ponto de ângulo .
Com essas informações, podemos esboçar o gráfico.
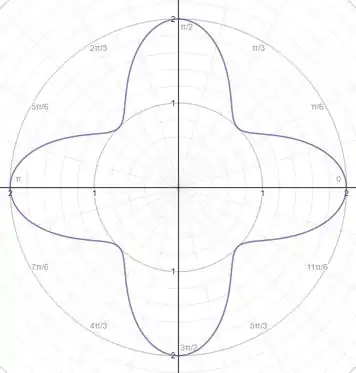
Resposta
A função é igual a: