Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.4 - Ex. 89
O flash de uma câmera armazena a carga de um capacitor e a dispara instanteneamente quando ativada. Os dados a seguir descrevem a carga remanescente no capacitor (medida em microcoulombs, ) no instante (medido em segundos).
a) Use uma calculadora ou computador para encontrar um modelo exponencial para a carga.
b) A derivada, representa a corrente elétrica (medida em microampère, ) que flui do capacitor para a lâmpada do flash. Use a parte (a) para estimar a corrente quando s.
Passo 1
Eaee, belezinha??
Bom... Essa é uma questão que exige o uso de um computador para fazer um ajuste de uma função.
É dado um conjunto de pontos mostrados na seguinte tabela:
Em que descreve a carga remanescente no capacitor (em ) em um flash de uma câmera fotográfica logo após o disparo que letva um tempo (em segundos).
Devemos achar uma função exponencial que os descreva bem.
Para isso, pode-se usar o método dos mínimos quadrados aprendido nos cursos de cálculo numérico, o método de linearização visto nos cursos de física experimental ou até mesmo recorrer diretamente a um software de computador.
Como o foco desse livro não é tratamento de dados nem análise numérica, vamos recorrer ao computador.
Passo 2
Fazendo um ajuste com uma função do tipo , obtemos
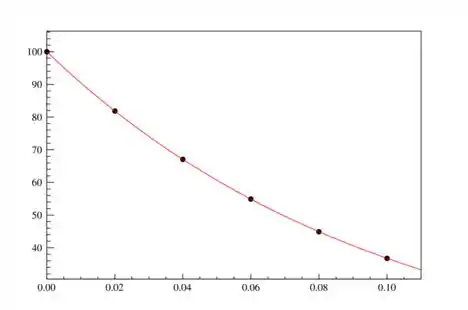
Os valores aproximados para os parâmetros foram e . Assim, temos que a função ajustada é
Passo 3
Obtemos derivando a expressão encontrada no passo 2 para calcular a corrente elétrica:
Assim, fazendo s, temos que
Resposta
a)
b)