Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 8.4 - Ex. 4

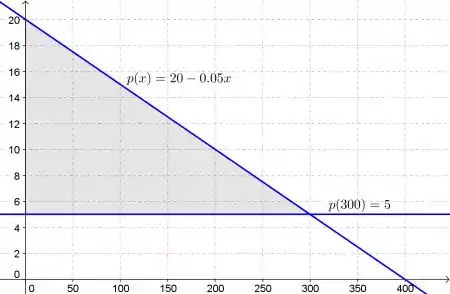
A função demanda para um certo produto é . Calcule o excedente do consumidor quando o nível de venda é . Ilustre desenhando a curva de demanda e identificando o excedente do consumidor como uma área.

Passo 1

Boa galera, nessa questão queremos calcular o excedente do consumidor no nível de venda dado.

Para isso, utilizaremos a integral e depois iremos esboçar a curva de demanda e identificar o excedente como uma área.

O excedente do consumidor é a região à esquerda da interseção entre a função de demanda e o preço para um nível de vendas de 300, .

Passo 2

O excedente, chamado de será então

Substituindo na integral, temos

Resolvendo a integral, obtemos o seguinte resultado

Passo 3

Aplicando os limites de integração, temos o excedente

Esboçando a curva graficamente temos o seguinte gráfico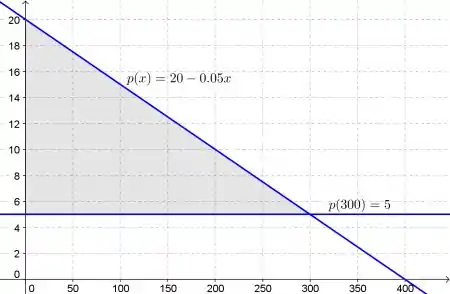

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse F ( x ) por partes, de forma que não envolva uma integral. F x = ∫ - 1 x t d t

Expresse F ( x ) por partes, de forma que não envolva uma integral. F x = ∫ 0 x f ( t ) d t , onde f ( x ) = x ,0 ≤ x ≤ 22 ,x2

Qual é o domínio natural da função F x = ∫ 1 x 1 t 2 - 9 d t Explique seu raciocínio.

Encontre todos os valores de x * no intervalo dado cuja existência é garantida pelo Teorema do Valor Médio para Integrais e explique o que esses números representam.(a) f x = x ; 0,3 (b) f x = 1 x ; [

Um tumor de 10 g é descoberto em um rato de laboratório em 1º de março. O tumor cresce a uma taxa de r ( t ) = t / 7 gramas por semana, onde t denota o número de semanas desde 1º demarço. Qual será a