Identifique a superfície com a equação dada. ρ = cos ⁡ ϕ

Essa é a equação de uma esfera de raio 1 / 2 e centrada em ( 0,0 , 1 / 2 ) .

Enunciado

E aiiiii minha turma, tudo bem? Vamos começar!!!

Precisamos identificar a superfície a partir da seguinte equação dada:

Vish, agora lascou! Como faço essa??

Calma, vamos pensar juntos.

Repara que essa nomenclatura lembra muito coordenadas esféricas né!?

Vamos lembrar como é coordenadas esféricas. Pegamos um ponto na esfera, e descremos as coordenadas , e :

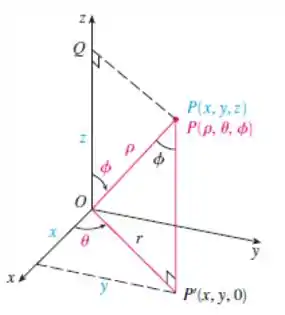
Das equações de transformação para coordenadas esféricas, temos:

Sabendo disso, nosso passo é fazer o caminho inverso. Vamos achar uma relação da expressão dada com as expressões em coordenadas esféricas.

Bora lá!!!

Podemos multiplicar a equação dada por dos dois lados, sendo assim, temos:

Vamos observar a expressão da esfera:

Observa que temos um , certo? Então vamos substituir. Ficamos com:

Agora repara como é descrita em coordenadas esféricas a componente :

Perceba que podemos reescrever a expressão:

Substituindo, por .

Fazendo isso, vamos ter:

Agora iremos somar dos dois lados para completar quadrados em :

Assim, temos:

Essa é a equação de uma esfera de raio e centrada em .

Essa é a equação de uma esfera de raio e centrada em .