Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.4 - Ex. 72
Ilustre a regra de L’Hospital fazendo o gráfico de e próximo de , para ver que essas razões têm o mesmo limite quando . Calcule também o valor exato do limite.
e
Passo 1
E aí, tudo bom?! Aqui temos a função:
Devemos fazer o gráfico de:
E localizar o ponto .
Essa é uma questão muito interessante, o objetivo aqui é estimar o valor de:
Mostrando que:
Que é a regra de L’Hospital, ou seja, vamos provar na na prática que a regra de L’Hospital funciona!
Depois disso vamos usar a regra de L’Hospital pra calcular o valor de:
Vamos lá?!
Passo 2
Vamos plotar primeiro a razão:
Temos que:
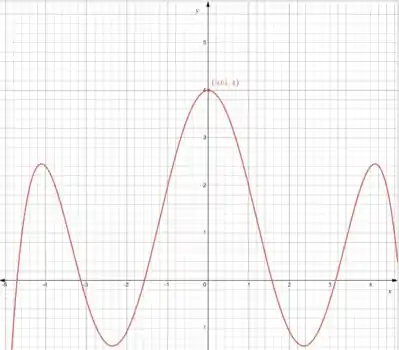
Assim tende a zero, então quando tende a . No ponto a função é indefinida, pois:
Passo 3
Agora precisamos plotar a curva de:
Primeiro vamos calcular as derivadas:
Pra calcular a gente usa a regra do produto:
Agora :
Agora vamos plotar:
O gráfico dessa razão é:
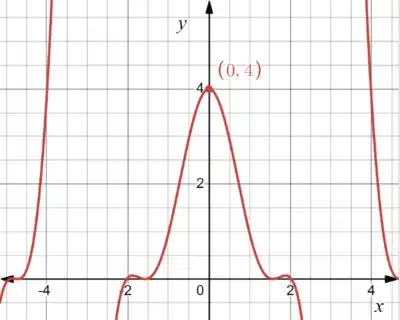
Opaaa...então vemos que quando se aproxima de , então:
Ou seja:
Passo 4
Agora vamos calcular o valor do limite explicitamente. A derivada já ta calculada, então só temos que substituir:
Aweee, exatamente o mesmo ponto que achamos nos gráficos!