Enunciado
Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.6 - Ex. 4
A instrução para a integral , têm duas partes, uma para a regra do trapézio e uma para a regra de Simpson.
Passo 1
Para a realização desta questão é pertinente que relembremos a regra do trapézio e a regra de Simpson para integrais.
A regra do trapézio utiliza de trapézios no lugar de retângulos para estimar uma integral definida f, de a até b. Além disso, calculamos T no lugar da integral f, sendo T dado por:
T = (y0 + 2y1 + 2y2 + ... + 2yn-1 + yn)
A regra de Simpson utiliza um sistema de troca parecido, no entanto, são usadas parábolas. E para o seu cálculo apresentamos a letra S no lugar da integral f, sendo S dado por:
S = (y0 + 4y1 + 2y2 + 4y3 + ... + 2yn-2 + 4yn-1 + yn)
OBS: O tamanho da malha (comprimento do subintervalo), é relacionado por: = (b – a)/n
Passo 2
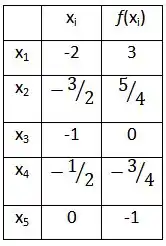
(a) = =
T = (3 + 2 * + 2 * 0 + 2 * + (-1))
T = (3 + + 0 + + (- 1))
T = (3) =
f(x) = x2 – 1 => f’(x) = 2x => f”(x) = 2;
Logo o M = 2 e ET 2 =
OBS : O limite superior é um valor do “pior caso”, de modo que f”(x) ≤ M em [a,b]. E para determiná-lo substituímos o xi que levaria ao maior valor correspondente na segunda derivada.
Para a letra (b), devemos calcular a integral de forma direta (aplicada na fórmula tradicional), e encontrar ET (ET = – T).
(b) dx
=
= 0 =
ET = – T = - = =
Em relação a letra (c), precisamos somente aplicar a fórmula administrada.
(c) * 100 = * 100 ≈ 13%
Passo 3
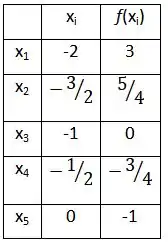
(a) = =
S = (3 + 4 * + 2 * 0 + 4 * + (-1))
S = (3 + 5 + 0 + (-3) + (-1))
S = (4) =
f(x) = - 1 => f’(x) = 2x => f”(x) = 2 => f(4)(x) = 0
Logo o M = 0 e ES = 0
OBS : O limite superior é um valor do “pior caso”, de modo que f(4)(x) ≤ M em [a,b]. E para determiná-lo substituímos o xi que levaria ao maior valor correspondente na quarta derivada.
Para a letra (b), devemos calcular a integral de forma direta (aplicada na fórmula tradicional), e encontrar ES (ES = – S).
(b) dx
=
= 0 =
ES = – S = = 0
Em relação a letra (c), precisamos somente aplicar a fórmula administrada.
(c) * 100 = * 100 = 0%
Resposta
Ei, a resposta está no passo a passo :)