Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 6.15 - Ex. 14e
Investigar as integrais impróprias.
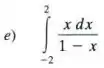
Passo 1
Uma integral representa a área sob a curva da dada função que está como o integrando. A integral imprópria possui o mesmo ideal, no entanto ela é representada por uma área indefinida, visto que o intervalo de integração possui pelo menos um valor em que a função não está definida.
Por conta disso, a integral não pode ser resolvida diretamente, necessitando da aplicação de um limite e da substituição do intervalo de integração por um intervalo que conterá uma nova variável, esta que irá tender ao valor para o qual a função não é definida.
Quando o valor no qual isso ocorre é um número inteiro, deve-se verificar os limites laterais a esse ponto para verificar se o limite existe ou não.
Passo 2
Para os casos em que o intervalo de integração vai de a , deve-se dividir a integral original em duas integrais intermediárias separadas no valor em que a função não existe. Assim, ela resultará em:
E, como a função é indefinida em , tem-se:
Resolvendo a integral por substituição simples fazendo e , obtém-se:
Separando em duas integrais:
E retornando à variável original:
Analisando o primeiro limite apenas e substituindo os limites de integração, podemos ter:
Passo 3
Ainda, dependendo do resultado da integral imprópria é possível tirar duas conclusões sobre o seu comportamento: caso o resultado seja um número inteiro, então o limite existe e a integral converge (é convergente); caso contrário e ela resulte em , o limite não existe e a integral diverge (é divergente).
Para este caso, visto que um dos limites não existe, não é necessário resolver o outro limite já que isso torna a integral divergente.
Resposta
A integral é divergente.