Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.4 - Ex. 7
Para o limite
ilustre a Definição encontrando os valores de que correspondam a e .
Passo 1
Olá, meu amado aluno. Estarei te ajudando a resolver essa atividade aqui, pega seu lápis e seu caderno que vamos começar.
O enunciado nos da :
E pede pra a gente ilustrar a definição a encontrando os valores de que correspondam a e . Os valores , e vem da definição do limite.
Relembrando o que a definição 2 diz que:
Seja uma função definida sobre algum intervalo aberto que contém o número , exceto possivelmente no próprio . Então dizemos que o limite de quando tende a é , e escrevemos:
Se para todo o número houver um número tal que se então .
Basicamente ela nos diz o quão próximo nossa função fica de um valor limite ao ficarmos de distancia de um valor . Então iremos utilizar a definição e encontrarmos esses valores. Vamos utilizar das propriedades de modulo para que possamos escolher quais valores ficam próximos como a questão quer.
Passo 2
Para , a definição de um limite requer que ache um tal que
O que implica em:
e
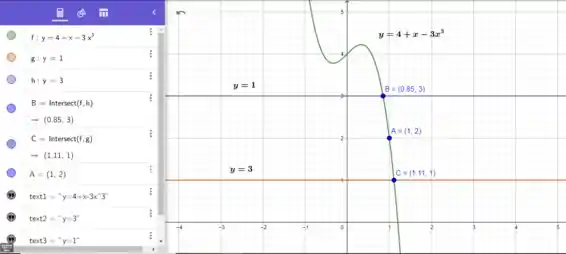
A função está entre as linhas (extremidades) e , e as coordenadas dos pontos de interseção da função com essas linhas são e . Portanto,
Como consideramos a área perto do ponto , a distância entre dessas extremidades é e respectivamente. Escolhemos um valor menor para o nosso , que é o número .
No gráfico abaixo você pode constar o que analisado acima.
Passo 3
Para , a definição de um limite requer que ache um tal que
Reescrevendo essa desigualdade, primeiro retirando o modulo:
Passando o 2 para ambos os lados da desigualdade:
O que implica em:
se
Se plotarmos o gráfico de , e , vamos achar que:
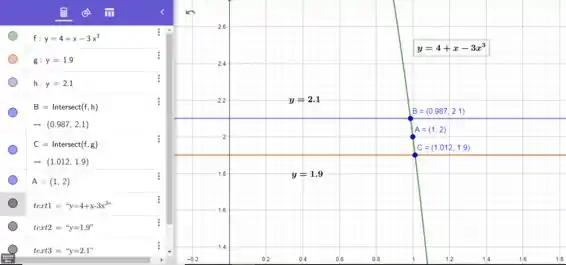
Vemos que a distância até a extremidade esquerda é , e a distância até a extremidade direita é .
Podemos escolher como o menor desses números, isto é . Embora tenhamos escolhido , qualquer valor menor positivo de também funcionaria.
Resposta
Desenvolvimento acima.