Para o limite , use um gráfico para determinar o valor do correspondente a .
Usando um sistema de computação algébrica para resolver a equação , determine o maior valor possível para que funcione para qualquer dado.
Tome na sua resposta da parte (b) e compare com a sua resposta da parte (a).
Passo 1
Olá, meu amigo, Yuri aqui e eu e você iremos juntos resolvermos essa atividade de limites.
Em todas as alternativas dessa questão aparecem duas variáveis: e . Você lembra que variáveis são essas?
Isso nos remete a definição de limites, e é também por esse caminho que iremos atuar.
Dizemos que , se para qualquer número real positivo , existe um número real positivo tal que, sempre que , então .
Essa definição pode ser lida da seguinte forma: para qualquer pequena margem de erro que você escolher, existe uma vizinhança ao redor de tal que, se estiver dentro dessa vizinhança, então estará dentro da margem de erro de .
A alternativa nos pede para encontramos o valor de para um determinado .
Então precisamos determinar tal que:
Passo 2
a) Com a ajuda do GeoGebra criamos o gráfico da função:
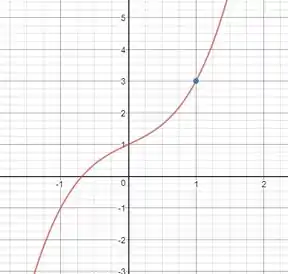
Estamos então interessados na região do ponto destacado na figura.
Reescrevendo nossa inequação utilizando os conceitos de limites:
Tirando do módulo:
Então, precisamos determinar os valores de para os quais a curva está entre as linhas e . Portanto, nós traçamos as curvas , e próximas ao ponto .
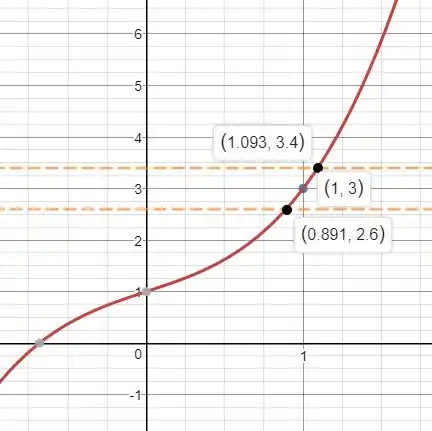
Então usamos o cursor para estimar a coordenada x da interseção da linha com a curva e, de maneira semelhante, a coordenada x da interseção da linha com a curva :
O intervalo não é simétrico em relação a . A distância de até o ponto de extremidade esquerdo é , e a distância até o ponto de extremidade direito é . Podemos escolher como o menor entre esses números:
Passo 3
b) Utilizando do nosso querido wolfram alpha para resolver essa alternativa, obtemos 3 raízes pois temos uma equação de grau 3, porém neste caso apenas obtemos uma raiz real:
A maior valor possível de δ é .
Passo 4
c) Se
o que concorda com a resposta de (a).
Resposta
.
e , o que concorda com a resposta de (a).