Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.5 - Ex. 17

int (x^4 + 3 x^3 - 5 x^2 - 4 x + 17)/(x^3 + x^2 - 5 x + 3) d x

Passo 1

Primeiro vamos dividir o numerador pelo denominador para achar uma função com o denominador com o grau maior que o do numerador.

(x^4 + 3 x^3 - 5 x^2 - 4 x + 17)/(x^3 + x^2 - 5 x + 3)

A nossa divisão fica assim

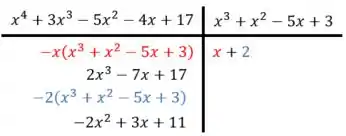
Assim podemos rescrever

(x^4 + 3 x^3 - 5 x^2 - 4 x + 17)/(x^3 + x^2 - 5 x + 3) = x + 2 + (- 2 x^2 + 3 x + 11)/(x^3 + x^2 - 5 x + 3)

Então a nossa integral fica

int ( x + 2 ) + (( - 2 x^2 + 3 x + 11 ))/(( x^3 + x^2 - 5 x + 3 )) d x

Logo

int ( x + 2 ) d x + int (( - 2 x^2 + 3 x + 11 ))/(( x^3 + x^2 - 5 x + 3 )) d x

Primeiro vamos arranjar a equação de forma mais conveniente para resolver as frações parcias. Esse passo é feito manipulando as funções, fazendo que ela fique de forma mais agradável para gente, geralmente usamos as raízes para reescrever as equações.

int (( - 2 x^2 + 3 x + 11 ))/((x - 1)^2 ( x + 3 )) d x

Passo 2

Agora vamos para frações parciais, temos que:

(( - 2 x^2 + 3 x + 11 ))/((x - 1)^2 ( x + 3 )) = (A)/((x - 1)^2) + (B)/((x - 1)) + (C)/(( x + 3 ))

Isolando - 2 x^2 + 3 x + 11 , vamos achar

- 2 x^2 + 3 x + 11 = A (x + 3) + B (x - 1) (x + 3) + C (x - 1)^2

Resolvendo o sistema de equações acima, temos:

A = 3 ; B = - 1 ; C = - 1

Agora substituindo os valores de A, B e C, temos:

(( - 2 x^2 + 3 x + 11 ))/((x - 1)^2 ( x + 3 )) = (3)/((x - 1)^2) + (- 1)/((x - 1)) + (- 1)/(( x + 3 ))

Passo 3

Já resolvemos as frações parciais, agora só falta resolver a integral.

int (( - 2 x^2 + 3 x + 11 ))/(( x^3 + x^2 - 5 x + 3 )) d x = (int (3)/((x - 1)^2) d x + int (- 1)/((x - 1)) d x + int (- 1)/(( x + 3 )) d x)

Ficou fácil agora, basta resolver as integrais, que são bem simples.

int (( - 2 x^2 + 3 x + 11 ))/(( x^3 + x^2 - 5 x + 3 )) d x = - 3 // ( - 1 + x ) - l n | 1 - x | - l n | 3 + x |

Resposta

int (x + 2) d x + int ((- 2 x^2 + 3 x + 11))/(( x^3 + x^2 - 5 x + 3 )) d x = - (3)/(- 1 + x) - x + (1)/(2) (3 + x)^2 - ln |1 - x| - ln |3 + x| + c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral int (4 x)/(x^3 + x^2 + x + 1) d x
Calcule a integral int (a x)/(x^2 - b x) d x
Calcule a integral int (x^5 + x - 1)/(x^3 + 1) d x
Calcule a integral.11.int_0^1 (2)/(2 x^2 + 3 x + 1) d x
Calcule a integral int (x^2 + 1)/((x - 3) (x - 2)^2) d x