Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 22

Mostre que uma cônica com foco na origem, excentricidade e diretriz tem a equação polar

Passo 1

Beleza, pessoal? Primeiro, vamos fazer um esboço do que seria uma cônica com foco na origem, excentricidade e diretriz , beleza?

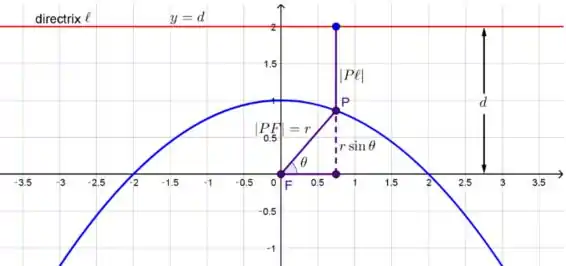
Agora, como provar que essa cônica tem a seguinte equação?

Passo 2

Galera, vamos lembrar de como definimos uma cônica: a razão entre a distância de um ponto qualquer da cônica ao foco e a distância entre esse ponto e a reta diretriz deve ser igual à excentricidade:

Digamos que o ponto tem coordenadas polares e retangulares .

Como mostra a figura, o foco está na origem, então .

Olhando novamente pra figura, vemos que

Como é positivo:

Passo 3

Agora que já temos e em coordenadas polares, jogamos esses valores na equação:

Show! Essa é a equação à qual queríamos chegar!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se um projétil for atirado com uma velocidade inicial v 0 metros por segundo com um ângulo α acima da horizontal e a resistência do ar for considerada desprezível, então sua posição, depois de t segun

Investigue, com o auxílio de uma ferramenta gráfica, a família de curvas definidas pelas equações paramétricas x = cos ⁡ t y = sen ⁡ t - sen ⁡ c t c0 Comece tomando c como um inteiro positivo e veja o

Investigue a família de curvas definidas pelas equações paramétricas x = t 2 y = t 3 - c t Como muda o formato quando c aumenta? Ilustre traçando vários membros da família com o auxílio de uma ferrame

As curvas com equações x = a sen ⁡ n t y = b cos ⁡ t São chamadas de figuras de Lissajous. Investigue, com o auxílio de uma ferramenta gráfica, como essas curvas mudam quando a , b e n variam. (Tome n

Elimine o parâmetro para encontrar uma equação cartesiana da curva: x = t y = 1 - t