Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 51
As curvas com equações
São chamadas de figuras de Lissajous. Investigue, com o auxílio de uma ferramenta gráfica, como essas curvas mudam quando , e variam. (Tome como um inteiro positivo).
Passo 1
Oie, amigo, tudo bem? Vou te ajudar a resolver essa atividade hoje.
Essa atividade é uma atividade para ser feita utilizando um software gráfico. Aqui a gente vai utilizar o Desmos, mas você pode utilizar qual software você gostar mais.
A gente vai primeiro plotar diversas curvas com valores diferentes de , assim a gente vai conseguir notar como o valor de , influencia. Para isso a gente precisa escolher um neutro.
Depois que a gente entender como , influencia, é hora de mudar os valores de e , e assim plotarmos diferentes valores, para analisarmos como e influenciam.
Passo 2
Vamos fazer o seguinte: como temos que avaliar a influência de coisas no comportamento da nossa curva, vamos primeiro fixar o e o e fazer variar o pra gente estudar primeiro como o influencia e depois a gente vê o e o tá bem?
Pra facilitar nossas vidas, vamos dizer que:
Assim:
Show, agora vamos chutar alguns valores pra e plotar isso.
Como é um inteiro positivo, vamos começar com :
Temos uma circunferência:
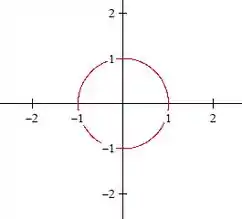
Agora, :
Aí o negócio já dá uma doideira e oscila, assim:
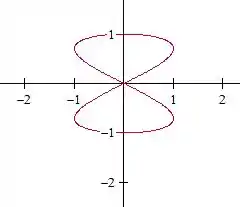
Vamos tentar :
Vish maria, ele oscilou mais ainda:
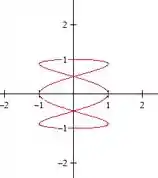
Vamos testar um maior só pra ter certeza, tipo :
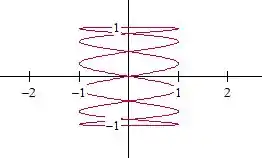
É, realmente, parece que esse negócio do controla a oscilação!
Passo 3
Show, agora que já descobrimos como afeta nossa curva, vamos para os parâmetros e .
Pra isso, vamos manter nosso .
Ora, acho que aí a gente não precisa nem plotar né? Só fazendo a gente vê que isso daí é a parametrização de uma elipse.
E na parametrização da elipse o controla o tamanho da nossa curva no eixo horizontal e o controla o tamanho da curva no eixo vertical.
Passo 4
Maas, como fazer prova real nunca é demais, vamos colocar e fazer o e variar uma vez pra ver se é isso mesmo.
Vamos fazer e :
Eu plotei junto com o caso em que para você ver a diferença:
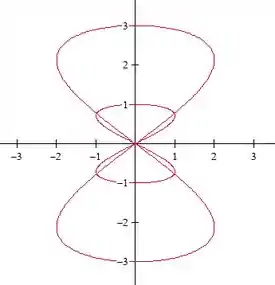
Tá vendo como a curva agora está cortando o em e antes ela cortava em ?
E tá vendo também como antes, quando , ela só ia até a altura de e agora, quando ela vai até a altura de ?
Pois é, então parece que estávamos certo desde o princípio.
Resposta
Quando aumenta, o número de oscilações da curva aumenta e cdetermina o tamanho da curva no eixo horizontal e o o tamanho da curva no eixo vertical.