Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.4 - Ex. 67
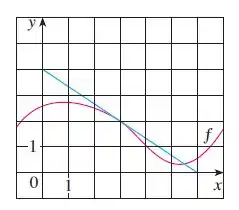
Se , onde o gráfico de f é mostrado, avalie .
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão deu pra gente o gráfico de uma função
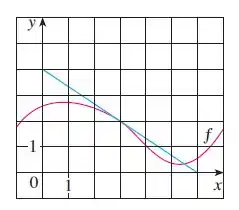
e disse que existe uma função definia por:
Precisaremos calcular .
Perceba que o que precisamos é da derivada da função avaliada no ponto .
Como está “dentro” de , pensamos nela como numa função composta. E para encontrar sua derivada usamos a Regra da Cadeia.
Assim, vamos chamar:
E:
Então:
Agora que já sabemos por onde começar, vem comigo que te mostro o desenrolar dessa história.
Passo 2
Vamos começar derivando em função de u:
Agora, u em relação a x:
Sendo assim:
Substituindo u:
Show. Já temos nossa expressão da derivada.
Passo 3
Mas nós queremos a derivada quando
Assim, basta fazer a substituição do valor de diretamente na expressão da derivada e teremos:
Pelo gráfico podemos obter que:
Agora nós precisamos achar
Aqui é muito importante lembrarmos que a derivada da função em um determinado ponto fornece a inclinação da reta tangente.
Então ficou fácil! Se sabemos que:
Para descobrir a inclinação da reta tangente basta usarmos a equação da reta:
Reorganizando:
Agora observe o gráfico
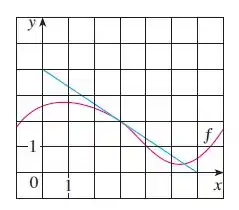
Pelo gráfico sabemos que:
Então:
Se sabemos a inclinação, então
Passo 4
Agora é só substituir e pronto!
Simplificando, teremos
E prontinho! Questão resolvida.