Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 1.1 - Ex. 21
Um pequeno lago contém, inicialmente, de galões (aproximadamente litros) de água e uma quantidade desconhecida de um produto químico indesejável. O lago recebe água contendo dessa substância por galão a uma taxa de galões por hora. A mistura sai à mesma taxa, de modo que a quantidade de água no lago permanece constante. Suponha que o produto químico esteja distribuído uniformemente no lago.
- Escreva uma equação diferencial para a quantidade de produto químico no lago em um instante qualquer.
- Qual a quantidade do produto químico que estará no lago após um período muito longo de tempo?
Passo 1
Para resolvermos esse problema vamos analisar as informações dadas no enunciado e tentar descrever uma equação que satisfaça todos os requisitos do problema. Além disso, para esse caso especifico, vamos nos atentar a unidade que usaremos para o problema, que será galões. Vamos juntos!!
Passo 2
- Bom, o enunciado nos diz algumas informações sobre o problema. Ele nos diz que entra galões por hora com a substância indesejável e que essa mesma substância sai à mesma taxa porém do valor total da água em todo lago. Assim, temos que a equação ficará da forma
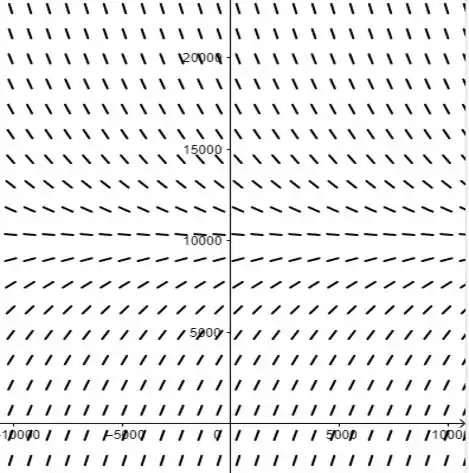
Passo 3
Vemos pelo campo de direções que todas as soluções tendem, para um muito grande, de produto químico.