Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.5 - Ex. 65

Prove que lim x → + ∞ ⁡ 6 - x - x 2 = - ∞ aplicando a definição do exercício 63 a

Definição: lim x → + ∞ ⁡ f x = - ∞ se a função f estiver definida em algum intervalo a , + ∞ e se para todo N < 0 existir um M > 0 tal que se x > M então f x < N .

Passo 1

Pra provar essa afirmação ai galera, vamos primeiro trocar x por M na expressão da função e definir isso como o valor de N. Logo:

N = f M = 6 - M - M 2

Pra provar que f x < N basta substituirmos o valor de N escolhido:

6 - x - x 2 < 6 - M - M 2

- x - x 2 < - M - M 2

x 2 + x > M + M 2

x 2 + x - M + M 2 > 0

Como do lado direito temos um polinômio do segundo grau do tipo:

a x 2 + b x + c = x 2 + x - M + M 2

Sendo a > 0 , podemos afirmar que todo o polinômio x 2 + x - M + M 2 só será positivo para

x > x 1

x < x 2

Onde x 1,2 são as raízes do polinômio, tais que:

x 1 , 2 = - b ± b 2 - 4 a c 2 a

x 1 > x 2

Para x > x 1 , tomamos a maior raiz e ficamos com:

x > - 1 + 1 + 4 M + M 2 2

x > - 1 + 4 M 2 + 4 M + 1 2

x > - 1 + 2 M + 1 2 2

x > - 1 + 2 M + 1 2

x > 2 M 2

x > M

E veja só, x > M apareceu! Graficamente:

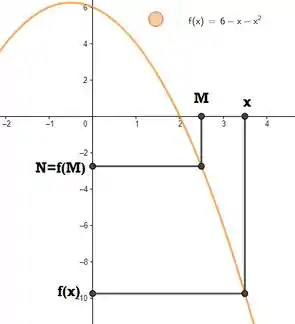
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os limites nos Exercícios 23-42. lim x → 9 ⁡ x - 3 x - 9
Determine os limites nos Exercícios 23-42. lim t → 1 ⁡ t 2 + t - 2 t 2 - 1
Determine os limites nos Exercícios 43-50. lim x → - π ⁡ x + 4 cos ⁡ ( x + π )
Determine os limites nos Exercícios 43-50. lim x → 0 ⁡ ( 2 sen ⁡ x - 1 )
Determine os limites nos Exercícios 23-42. lim x → - 2 ⁡ x + 2 x 2 + 5 - 3