Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.4 - Ex. 17

Utilize a integral dupla para determinar a área da região.

A região dentro do círculo x - 1 2 + y 2 = 1 e fora do círculo x 2 + y 2 = 1 .

Passo 1

Faala, pessoal!

Nessa questão, precisamos calcular a área de uma região usando integral dupla. Usamos essa relação pra isso:

A D = ∬ D d A

Como nossa região é circular, vamos usar coordenadas polares:

x = r cos ⁡ θ y = r sen ⁡ θ

Não podemos esquecer do jacobiano!!! Pra coordenadas polares é

J = r

Então, vamos começar desenhando a região, e definindo os limites de integração de r e θ .

Daí, calculamos a integral e achamos o valor da área.

Passo 2

Nossa região D é a região dentro do círculo x - 1 2 + y 2 = 1 e fora do círculo x 2 + y 2 = 1 .

Eles são círculos de raio 1 um centrado na origem e outro no ponto 1,0 . Desenhando, temos:

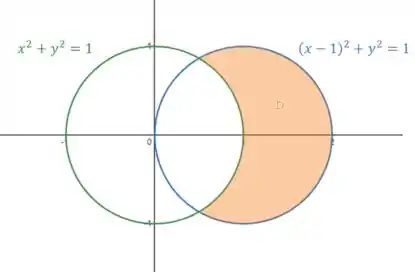
Vamos reescrever as equações em coordenadas polares:

x = r cos ⁡ θ y = r sen ⁡ θ

O círculo centrado na origem ( x 2 + y 2 = 1 ) por definição é:

r = 1

E o outro:

x - 1 2 + y 2 = 1

r cos ⁡ θ - 1 2 + r 2 sen 2 ⁡ θ = 1

Abrindo o quadrado:

r 2 cos 2 ⁡ θ - 2 r cos ⁡ θ + 1 + r 2 sen 2 ⁡ θ = 1

r 2 cos 2 ⁡ θ + r 2 sen 2 ⁡ θ - 2 r cos ⁡ θ = 0

Como sen 2 ⁡ θ + cos 2 ⁡ θ = 1 :

r 2 cos 2 ⁡ θ + sen 2 ⁡ θ - 2 r cos ⁡ θ = 0

r 2 - 2 r cos ⁡ θ = 0

Então

r r - 2 cos ⁡ θ = 0 ⇒ r = 0 ,         o u r = 2 cos ⁡ θ

Só que r = 0 não é uma curva... o único ponto com r = 0 é o 0,0 .

Então nossas curvas são

r = 1

r = 2 cos ⁡ θ

Passo 3

Bom, pelo nosso desenho, vemos que a nossa região está entre uma curva e outra. Para r isso significa que:

1 ≤ r ≤ 2 cos ⁡ θ

Para achar os limites de θ , vamos achar os pontos de interseção das duas curvas:

r = 1 r = 2 cos ⁡ θ

Então

1 = 2 cos ⁡ θ

cos ⁡ θ = 1 2 ⇒ θ = π 3 θ = - π 3

Esses são os nossos limites de θ , como vemos no desenho:

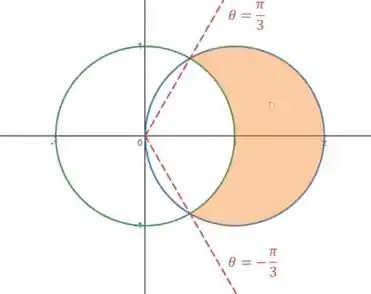
Ou seja:

1 ≤ r ≤ 2 cos ⁡ θ

- π 3 ≤ θ ≤ π 3

Passo 4

Agora voltamos pra integral

A D = ∬ D d A

Percebe que a integral mais de dentro vai ter que ser a de r , porque os limites dela dependem de θ . Além disso, vamos lembrar de colocar o jacobiano e:

= ∫ - π 3 π 3 ∫ 1 2 cos ⁡ θ r d r d θ

Fazemos essa integral de dentro pra fora. Primeiro em função de r , com θ constante:

= ∫ - π 3 π 3 ∫ 1 2 cos ⁡ θ r d r d θ =

= ∫ - π 3 π 3 r 2 2 1 2 cos ⁡ θ d θ =

Aplicando os limites de integração:

= ∫ - π 3 π 3 4 cos 2 ⁡ θ 2 - 1 2 d θ =

= ∫ - π 3 π 3 2 cos 2 ⁡ θ - 1 2 d θ =

Passo 5

Por último, integramos em função de θ :

= ∫ - π 3 π 3 2 cos 2 ⁡ θ - 1 2 d θ =

Vamos reescrever:

cos 2 ⁡ θ = 1 2 1 + cos ⁡ 2 θ

2 cos 2 ⁡ θ = 1 + cos ⁡ 2 θ

Então:

= ∫ - π 3 π 3 1 + cos ⁡ 2 θ - 1 2 d θ =

= ∫ - π 3 π 3 1 2 + cos ⁡ 2 θ d θ =

Integrando:

= θ 2 + sen ⁡ 2 θ 2 - π 3 π 3 =

= 1 2 π 3 + sen ⁡ 2 π 3 - - π 3 - sen ⁡ - 2 π 3 =

Como sen ⁡ 2 π 3 = 3 2 e sen ⁡ - 2 π 3 = - 3 2 ,

= 1 2 π 3 + 3 2 + π 3 + 3 2 =

= 1 2 2 π 3 + 3

Então:

A = π 3 + 3 2

Resposta

π 3 + 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região cuja área é dada pela integral e calcule-a. ∫ π / 2 π∫ 0 2 sen ⁡ θ r d r d θ
Use integral dupla e encontre a área da região. A região limitada por ambos as cardioides: r = 1 + cos ⁡ θ r = 1 - cos ⁡ θ
Calcule a integral dada, colocando-a em coordenadas polares.10. ∬ R y 2 x 2 + y 2 d A Onde R é a região que fica entre os círculos x 2 + y 2 = a 2 e x 2 + y 2 = b 2 com 0ab .
Calcule a integral dada, colocando-a em coordenadas polares.8. ∬ R 2 x - y d A Onde R é a região do primeiro quadrante limitada pelo círculo x 2 + y 2 = 4 e as retas x = 0 e y = x .
Calcule a integral dada, colocando-a em coordenadas polares.12. ∬ D cos ⁡ x 2 + y 2 d A Onde D é o disco com centro na origem e raio 2.