Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.5 - Ex. 8
Determine a massa e o centro de massa da lâmina que ocupa a região e tem função densidade .
é limitada por e ; .
Passo 1
Faala! Vamos ver o que essa questão quer:
Precisamos calcular a massa e o centro de massa de uma lâmina.
Nós temos a região que a lâmina ocupa e a função densidade
E é só disso que a gente precisa!
A massa é calculada assim:
E as coordenadas e do centro de massa assim:
Bom, já percebeu que primeiro calculamos , né? Porque e dependem dela.
Mas antes de mais nada, vamos ver quem é a região , pra conseguir definir os limites de integração e transformar essas integrais em integrais iteradas.
Passo 2
Então, nossa região está entre uma parábola e uma reta:
Vamos esboçar essa região:
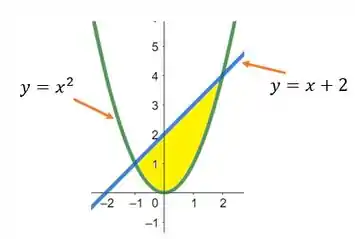
Assim, a região está acima da parábola ( maior do que o da parábola) e abaixo da reta ( menor do que o da reta):
Para determinar os limites de , precisamos achar os valores onde a parábola e a reta se interceptam:
Fazendo o sistema:
Resolvendo por Bhaskara:
Então os valores de que as curvas se interceptam são:
Como está entre esses dois pontos:
E assim temos os limites de e .
Observe que os limites de dependem de , então precisamos integrar primeiro em e depois em !!
Passo 3
Vamos começar calculando a massa da nossa região. Portanto, temos
Primeiro integramos em função de , considerando constante:
Calculando nos limites de integração:
Colocando em evidência pra fora da integral (por ser constante) e abrindo o quadrado:
E agora integramos em função de :
Resolvendo as contas:
Colocando todos os termos no mesmo denominador:
E achamos o valor da massa:
Passo 4
Agora, vamos calcular cada uma das coordenadas do centro de massa. Começando pela coordenada , temos:
Primeiro integrando em função de , mantendo constante:
O podemos colocar pra fora de todas as integrais, porque é constante e o pra fora dessa primeira, porque é constante em função de :
Resolvendo nos limites de integração:
Colocando em evidência pra fora e abrindo o quadrado:
E integramos em função de :
Simplificando:
Colocando no mesmo denominador:
Passo 5
Para a coordenada , o processo é o mesmo:
Primeiro integrando em função de , considerando constante:
Podemos tirar o da integral toda, já que é constante, e calcular:
Calculando nos limites:
Podemos colocar o em evidência pra fora da integral:
E agora vamos integrar em função de . Pra isso a gente poderia abrir esse cubo da soma... Mas tem uma outra forma, pra não precisar abrir muita conta. A gente vai dividir essa integral na soma de duas integrais:
Pra primeira integral, a gente pode fazer uma substituição
Então:
E agora conseguimos integrar normalmente:
Resolvendo as contas:
Simplificando:
Então encontramos nosso centro de massa:
Resposta
Massa:
Centro de massa: