Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.5 - Ex. 79
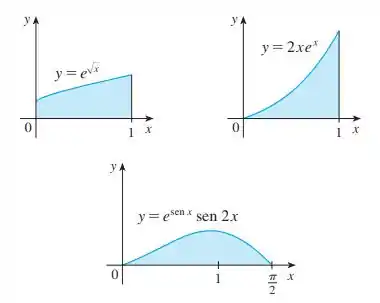
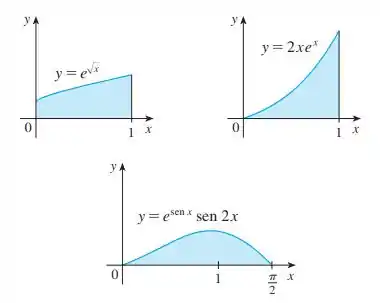
Quais das seguintes áreas são iguais? Por quê?
Passo 1
Opa, bora resolver esse problema! Queremos descobrir quais das seguintes áreas são iguais:
E para isso, vamos usar a integração.
Sabemos que a área abaixo de uma curva indo de um ponto até um ponto é calculada pela integral:
Passo 2
Analisando a primeira figura:
Para resolver essa integral vamos usar a técnica da substituição.
Se chamarmos o que está no expoente de teremos uma exponencial de uma variável pura, o que facilita a integração depois.
Devemos calcular então a diferencial , para isso derivamos :
Só que dessa forma, continuaremos com após a substituição! E isso não pode acontecer.
A saída aqui vai ser a seguinte, vamos primeiro escrever de forma explícita.
Sabemos que:
Então, podemos dizer que:
Agora vamos encontrar a diferencial derivando :
De forma que temos:
Agora sim teremos tudo em função de após a substituição.
Para calcular os novos limites de integração, temos que quando:
E que quando
Dessa forma, a integral vira:
E é isso, por enquanto não temos ferramentas para sair daqui.
Passo 3
Analisando a segunda figura:
Repara que essa deu um resultado que é exatamente igual ao que encontramos no Passo 2.
Ou seja, já podemos dizer que:
Passo 4
Analisando a terceira figura:
Vamos usar a técnica da substituição aqui.
Nesse caso, vamos escolher
Pois assim, a exponencial fica sendo sobre um único termo o que facilita a integração (e deixa essa integral parecida com as anteriores).
Ao fazer isso, temos que a diferencial de será:
Logo,
Mas não temos nenhum cosseno na nossa integral.
Para resolver isso, vamos usar a seguinte identidade trigonométrica.
Temos que a soma de arco no seno é dada por:
E para o caso de:
Isso deve ajudar.
Além disso, para os limites de integração, faremos que quando:
E que quando:
Assim, nossa integral fica:
Assim, temos que , todas as áreas são iguais.
Resposta
.