Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.7 - Ex. 1

Seja S o cubo com vértices ± 1 , ± 1 , ± 1 . Aproxime ∫ ∫ S x 2 + 2 y 2 + 3 z 2   d S   usando as somas de Riemann como na Definição 1, tomando os retalhos S i j como os quadrados que são as faces do cubo e os centros desses quadrados como os pontos P i j * .

Passo 1

E aí, galera! Tranquilo?

A questão pede para usarmos a soma de Riemann para achar o valor aproximado de:

∫ ∫ S x 2 + 2 y 2 + 3 z 2   d S

Onde S é o cubo com vértices ± 1 , ± 1 , ± 1 . Pela definição 1 temos que:

∫ ∫ S f x , y , z d S = lim m , n → ∞ ⁡ ∑ i = 1 m ∑ j = 1 n f P i j *   Δ S i j

Então aqui temos:

f x , y , z = x 2 + 2 y 2 + 3 z 2

Então, faremos o somatório de:

f P i j * ∆ S i j

Para cada retalho, onde:

f P i j *

É a função no ponto central do retalho e

∆ S i j

É a área do retalho, que aqui é o quadrado que forma cada face do cubo. Então, vamos começar achando os centros das faces e calculando as áreas de cada superfície. Multiplicamos as duas e somamos para todas as faces.

Passo 2

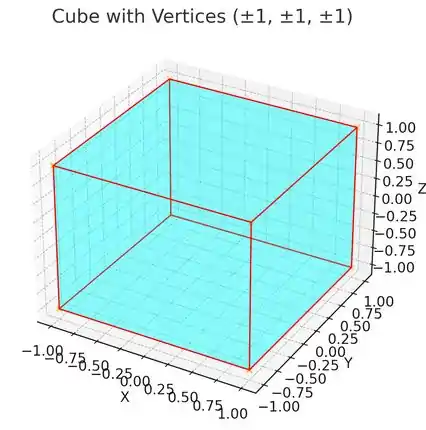
Pelos vértices do cubo:

± 1 , ± 1 , ± 1

Vemos que cada face medirá 2 unidades de medidas, já que os lados vão de - 1 até 1 . Cada face do cubo tem área igual a:

A = 1 - - 1 × 1 - - 1 = 4

E

f x , y , z = x 2 + 2 y 2 + 3 z 2

e P i j * são os pontos que cruzam com os eixos coordenados (que serão os centros dos quadrados). Olhando na imagem, podemos ver que os pontos centrais de cada face são:

  • 1,0 , 0
  • 0,1 , 0
  • 0,0 , 1
  • - 1,0 , 0
  • 0 , - 1,0
  • 0,0 , - 1

Passo 3

Dessa forma temos que a integral de superfície por integral de Riemann será a função nos pontos centrais, multiplicadas pela área, que é igual para todas as faces do cubo.

lim m , n → ∞ ⁡ ∑ i = 1 m ∑ j = 1 n f P i j *   Δ S i j = f 1,0 , 0 × 4 + f - 1,0 , 0 × 4 + f 0,1 , 0 × 4

+ f 0 , - 1,0 × 4 + f 0,0 , 1 × 4 + f 0,0 , - 1 × 4

Exemplificando a aplicação da função no ponto com o primeiro ponto da nossa soma:

f 1,0 , 0 = 1 2 + 0 + 0 = 1

Fazendo isso para todos os pontos, nossa soma será:

4 1 + 1 + 4 2 + 2 + 4 3 + 3 = 4 2 + 2 2 + 2 3 ≈ 33.17

Então:

∫ ∫ S x 2 + 2 y 2 + 3 z 2   d S ≈ 33.17

Resposta

∫ ∫ S x 2 + 2 y 2 + 3 z 2   d S ≈ 33.17

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da superfície.A parte da esfera x 2 + y 2 + z 2 = b 2 que está dentro do cilindro x 2 + y 2 = a 2 , onde 0ab .
Uma superfície que consiste do cilindro x 2 + y 2 = 1 ,- 1 ≤ z ≤ 1 , junto com seu fundo e tampa. Suponha que você saiba que f é uma função contínua com f ± 1,0 , 0 = 2 f 0 , ± 1,0 = 3 f 0,0 , ± 1 = 4
Seja H o hemisfério x 2 + y 2 + z 2 = 50 , z ≥ 0 , e suponha que f seja uma função contínua com f 3 ,4 ,5 = 7 , f 3 ,- 4 ,5 = 8 , f - 3 ,4 ,5 = 9 e f - 3 ,- 4 ,5 = 12 . Dividindo H em quatro retalhos,
Calcule a integral de superfície. ∫ ∫ S x yd S , S é a fronteira da região delimitada pelo cilindro x 2 + z 2 = 1 e pelos planos y = 0 e x + y = 2 .
Calcule a integral de superfície. ∫ ∫ S x 2 y + z 2 d S S é a parte do cilindro x 2 + y 2 = 9 entre os planos z = 0 e z = 2 .