Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.3 - Ex. 2

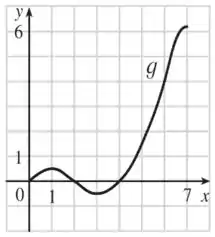
Seja g x = ∫ 0 x f t   d t em que f é a função cujo gráfico é mostrado.

(a) Calcule g x para x = 0 ,   1 ,   2 ,   3 ,   4 ,   5 ,   e   6 .

(b) Estime g 7 .

(c) Onde g tem um valor máximo? Onde possui um valor mínimo?

(d) Faça um esboço do gráfico de g .

Passo 1

Eaee, belezinha?? Bom... o enunciado nos dá o seguinte gráfico da função f :

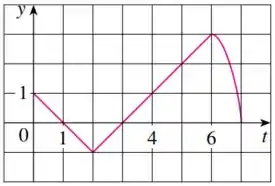
Além disso, a questão nos diz que:

g x = ∫ 0 x f t   d t

Queremos calcular g x para x = 0 ,   1 ,   2 ,   3 ,   4 ,   5 ,   e   6 .

Para isso, devemos substituir x na função dada e analisar o gráfico para podermos encontrar os valores dentro de cada intervalo.

Assim, lembre-se que a integral pode ser interpretada como a área sob a curva!!

Com isso, poderemos estimar o valor de g 7 .

Por fim, devemos analisar os valores de máximo e mínimo de g e esboçar seu gráfico!

Um bocadinho de coisa, né?? Mas vamos devagarinho que vai dar certo!! 😉

Passo 2

Item a:

Bom... vamos substituir o valor de x na função pelos valores que nos foram dados no enunciado e observar o gráfico da função para interpretar a integral como sendo a área sob o gráfico da função no intervalo pedido.

Para x = 0 , temos:

g 0 = ∫ 0 0 f t   d t = 0

Já que a integral começa e termna no mesmo lugar, não há área sob o gráfico.

Para x = 1 , temos o intervalo 0,1 que corresponde a um triângulo de base e altura iguais a 1.

Veja:

logo:

g 1 = ∫ 0 1 f t   d t = 1 2 1 1 = 1 2

Para x = 2 , temos:

g 2 = ∫ 0 2 f t   d t = ∫ 0 1 f t   d t + ∫ 1 2 f t   d t

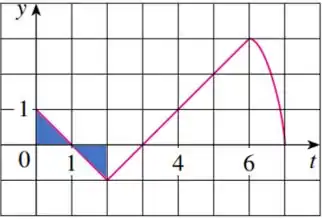
Perceba que são dois triângulos de base e altura iguais a 1 , porém existe um na parte positiva e outro na parte negativa, portanto:

g 2 = 1 2 - 1 2 = 0

Passo 3

Para x = 3 , temos:

g 3 = ∫ 0 3 f t   d t = ∫ 0 2 f t   d t + ∫ 2 3 f t   d t ∴

Perceba que já temos o resultado da integral do intervalo 0,2 .

Além disso, analisando o gráfico, a integral do intervalo 2,3 trata-se de um triângulo de base e altura iguais a 1 no lado negativo, portanto:

g 3 = 0 - 1 2 ∴

g 3 = - 1 2

Para x = 4 , temos:

g 4 = ∫ 0 4 f t   d t = ∫ 0 3 f t   d t + ∫ 3 4 f t   d t

Perceba que já temos o resultado da integral do intervalo 0,3 .

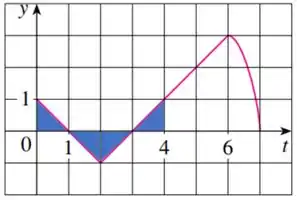
Além disso, analisando o gráfico, a integral do intervalo 3,4 trata-se de um triângulo de base e altura iguais a 1 no lado positivo, portanto:

g 4 = - 1 2 + 1 2 ∴

g 4 = 0

Passo 4

Para x = 5 , temos:

g 5 = ∫ 0 5 f t   d t = ∫ 0 4 f t   d t + ∫ 4 5 f t   d t ∴

Perceba que já temos o resultado da integral do intervalo 0,4 .

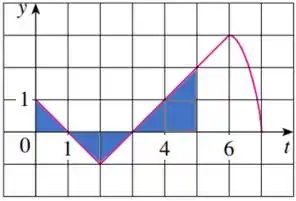
Além disso, analisando o gráfico, a integral do intervalo 4,5 trata-se de um quadrado de lado 1 e um triângulo de base e altura iguais a 1 no lado positivo, portanto:

g 5 = 0 + 1 2 + 1 * 1 2 ∴

g 5 = 3 2

Para x = 6 , temos:

g 6 = ∫ 0 6 f t   d t = ∫ 0 5 f t   d t + ∫ 5 6 f t   d t ∴

Perceba que já temos o resultado da integral do intervalo 0,5 .

E vamos seguir de forma análoga no preenchimento das áreas

Além disso, analisando o gráfico, a integral do intervalo 5,6 trata-se de dois quadrados de lado 1 e um triângulo de base e altura iguais a 1 no lado positivo, portanto:

g 6 = 3 2 + 1 2 + 1 2 + 1 * 1 2 ∴

g 6 = 8 2 ∴

g 6 = 4

Passo 5

Item b:

Para x = 7 temos:

g 7 = ∫ 0 7 f t   d t = ∫ 0 6 f t   d t + ∫ 6 7 f t   d t

g 7 = 4 + ∫ 6 7 f t   d t

Devemos estimar então, a área do gráfico entre x = 6 e x = 7 :

Podemos ver que a área da integral ∫ 6 7 f t   d t é maior que o triangulo de base 1 e altura 3 bem como é menor que o retângulo de mesma base e mesma altura, logo:

1,5 < ∫ 6 7 f t   d t < 3

Podemos estimar então, como a média do intervalo:

∫ 6 7 f t   d t ≈ 3 + 1,5 2 = 2.25

Então: o valor estimado de g 7 é

g 7 = 4 + ∫ 6 7 f t   d t ≈ 4 + 2,25

g 7 ≈ 6,25

Passo 6

Item c:

Pelos valores calculados em (a) e (b), podemos ver que g x tem máximo em x = 7 e mínimo em x = 3 .

Passo 7

Item d:

Analisando os valores de máximo e mínimo, bem como os demais valores de x que descobrimos na letra (a), o gráfico de g é esboçado por:

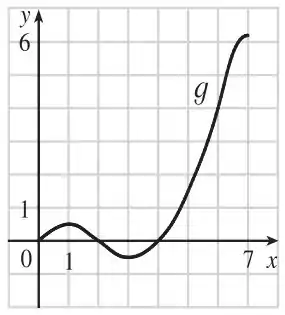
Entendeu direitinho?? Responde aee 😉

Resposta

(a) g 0 = 0, g 1 = 1 2 , g 2 = 0 , g 3 - 1 2 , g 4 = 0 , g 5 = 3 2 , g 6 = 4 .

(b) g 7 ≈ 6,25

(c) g x tem máximo em x = 7 e mínimo em x = 3 .

(d)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4. Calculec ) int_0^((pi)/(3)) (sin 3 x + cos 3 x) d x
5. b) Calcule int sin^2 x d x
6. Calculed ) int cos^2 (x)/(2) d x
6. Calculeb ) int cos^2 5 x d x
6. Calculef ) int ((1)/(2) + (cos 2 x)/(2))^2 d x