Seja a parte da esfera que está acima do plano . Se tiver densidade constante , encontre o centro de massa e o momento de inércia em torno do eixo .
Passo 1
Oi, galera, tudo bem?
Precisamos encontrar (a) o centro de massa e (b) o momento de inércia em torno do eixo da superfície definida pela região com parte da esfera:
Que está acima do plano
Com função densidade constante, ou seja:
Estamos trabalhando com essa regi��o aqui descrita nesse gráfico:
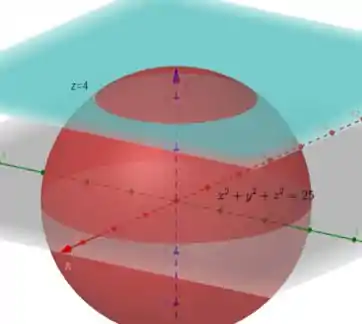
Para calcular as fórmulas do centro de massa e do momento de inércia, devemos calcular algumas integrais. Vamos por partes?
Passo 2
Para calcular o centro de massa, primeiro precisamos descobrir a massa dada por:
E quem é o ? Podemos calculá-lo assim:
Onde precisamos fazer as derivadas parciais de em relação a e a . Mas quem é nosso ?
Com o que temos no enunciado:
Assim,
Jogando na fórmula, teremos:
Organizando, teremos
Para calcular a massa, com a função densidade como uma constante , então
Para encontrarmos os limites de integração da região , lembre que (lá do enunciado), então
Em coordenadas polares,
Com isso, a região é definida por
Assim, teremos:
Colocando para fora da integral como constante...
Resolvendo de dentro para fora:
Passo 3
Agora iremos encontrar nossos centros de massa do item (a). São definidos por essas fórmulas aqui:
Por simetria, podemos dizer que as coordenadas e para o centro de massa serão . Portanto:
Organizando, teremos
Note que essa integral é basicamente a área da esfera, então:
Com isso, o centro de massa será dado por
Passo 4
Agora vamos calcular o momento de inércia em relação ao eixo para o item (b).
Sabemos que a expressão para o momento de inércia é:
Então temos com informações anteriores:
Organizando, teremos:
Colocando as constantes para fora da integral, e tendo como limites de integração (como já descobrimos para a massa)
Então, em coordenadas polares:
Reorganizando a integral de acordo com seus termos, chegaremos a
Para a primeira integral...
Para a segunda integral...
Por substituição,
Teremos:
Organizando, sabendo que
Assim, chegaremos a
Unindo todas as integrais, teremos: