Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.7 - Ex. 11

Seja D a região delimitada abaixo pelo plano z = 0 , acima pela esfera x 2 + y 2 + z 2 = 4 e dos lados pelo cilindro x 2 + y 2 = 1 . Monte as integrais triplas em coordenadas cilíndricas que fornecem o volume de D, utilizando as seguintes ordens de integração.

  1. d z   d r   d θ
  2. d r   d z   d θ
  3. d θ   d z   d r

Passo 1

Faaaala, cara! Tranquileba?

Fazendo um esboço da imagem das funções, teremos:

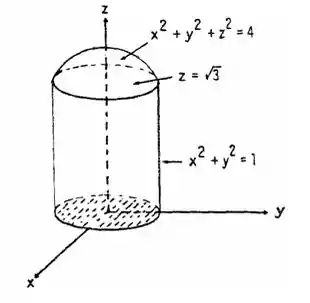
E por aqui já temos todas informações necessárias ara achar nossas respostas

Passo 2

Vemos que a giração de θ é por todo o espaço, logo:

0 ≤ θ ≤ 2 π

Para o raio, temos x 2 + y 2 = 1 , mas sabemos das coordenadas cilíndricas que r 2 = x 2 + y 2 de forma que:

0 ≤ r ≤ 1

E por ultimo temos que z vai de 0 até o limite em z - x 2 - y 2 logo:

0 ≤ z ≤ 4 - r 2

(usando que - r 2 = - x 2 - y 2 )

Passo 3

Não podemos nos esquecer do Jacobiano. Assim:

Para d z   d r   d θ :

∫ 0 2 π ∫ 0 1 ∫ 0 4 - r 2 d z   r   d r   d θ

Para d θ   d z   d r :

∫ 0 1 ∫ 0 4 - r 2 ∫ 0 2 π r   d θ   d z   d r

Para d r   d z   d θ :

∫ 0 2 π ∫ 0 3 ∫ 0 1 r   d r   d z   d θ + ∫ 0 2 π ∫ 3 2 ∫ 0 1 r   d r   d z   d θ

Resposta

Para d z   d r   d θ :

∫ 0 2 π ∫ 0 1 ∫ 0 4 - r 2 d z   r   d r   d θ

Para d θ   d z   d r :

∫ 0 1 ∫ 0 4 - r 2 ∫ 0 2 π r   d θ   d z   d r

Para d r   d z   d θ :

∫ 0 2 π ∫ 0 3 ∫ 0 1 r   d r   d z   d θ + ∫ 0 2 π ∫ 3 2 ∫ 0 1 r   d r   d z   d θ

Exercícios de Livros Relacionados

Escreva a equação em coordenadas cilíndricas.(a) 3 x + 2 y + z = 6 (b) - x 2 - y 2 + z 2 = 1
Escreva a equação em coordenadas cilíndricas.(a) z = x 2 + y 2 (b) x 2 + y 2 = 2 y
Esfera e paraboloide Encontre o volume da região delimitada acima pela esfera x2 + y2 + z2 = 2 e abaixo pelo paraboloide z = x2 + y2.
Como as integrais triplas são definidas em coordenadas cilíndricas e esféricas? Por que alguém poderia preferir trabalharem um desses sistemas de coordenadas a trabalhar em coordenadas retangulares?
Semicilindro infinito Seja D o interior de um semicilindro circular reto infinito de raio 1 , com sua extremidade suspensa a uma unidade acima da origem e seu eixo igual ao raio entre ( 0,0 , 1 ) e ∞