Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.7 - Ex. 1
Seja a superfície que é fronteira da caixa delimitada pelos planos e . Aproxime usando uma soma de Riemann, como na Definição , tomando os retalhos como os retângulos que são as faces da caixa e os pontos como os centros destes retângulos.
Passo 1
Fala, galera! Tranquilidade?
A questão pede pra calcularmos o valor aproximado de
Através da soma de Riemann como na Definição 1. Aqui, a superfície que é fronteira da caixa delimitada pelos planos e .
A Definição 1 traz que:
Então, faremos o somatório de:
Para cada retalho, onde:
É a função no ponto central do retalho e
É a área do retalho, que aqui é o retângulo que forma cada face da caixa. Então, vamos começar achando os centros dos planos e calculando as áreas de cada superfície. Multiplicamos as duas e somamos para todas as faces.
Passo 2
Vamos começar por uma face de cada vez, definindo os pontos centrais de cada e sua respectiva área:
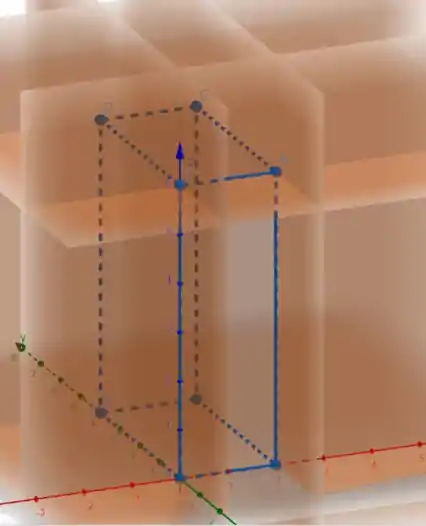
Planos e
- e
- e
- e
Galera, as faces da caixa nos planos e , como podemos ver na nossa imagem, tem 4 unidades em e 6 unidades em , então a área é:
Seu ponto central é metade a medida em , metade da medida em e os valores de já temos da própria equação dos planos.
centros
Agora usamos a mesma lógica que usamos para os planos em .
centros
centros
Passo 3
Agora precisamos calcular os pontos centrais na função, que no nosso caso é:
Por exemplo:
Então, faremos isso com todos os demais pontos centrais que achamos no passo 2. Agora, vamos aplicar nossa soma: somamos todos os pontos centrais multiplicados por suas respectivas áreas .
Assim, nossa integral dupla pela soma de Riemann pode ser aproximada por:
Calculando o valor da função no ponto e multiplicando pelo valor da área, com a ajuda de uma calculadora, chegamos em: