Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.5 - Ex. 9
9. Sejam .
a) Verifique que a imagem de está contida na curva de nível
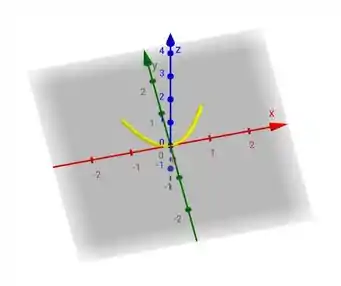
b) Desenhe a imagem de
c) Verifique que para todo t,
Passo 1
a)
Curva de nível
Então,
É uma parábola e a imagem de também é uma parábola.
Passo 2
b)
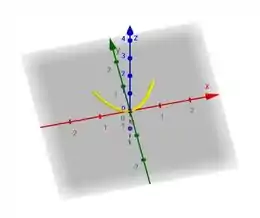É uma parábola que não tem altura em z.
Passo 3
c)
O gradiente é nada mais do que as derivadas parciais.
As derivadas parciais são nada mais nada menos do que derivar primeiro em x e considerar y como constante e depois derivar y e considerar x como constante.
Então, para a nossa questão, vamos derivar em x,
Agora vamos derivar em y,
Portanto, o gradiente de
Verificando,
Resposta
- Verificado, as duas funções tem mesma imagem.
- Verificado.
Exercícios de Livros Relacionados
É dada uma curva γ ( t ) cuja imagem é a intersecção das superfícies 4 x 2 + y 2 = 1 e x + y + z = 1 . Suponha γ t 0 = ( 0 ,1 ,0 ) e γ ' t 0 ≠ 0 → .a) Determine a reta tangente a γ em γ ( t 0 ) .b) De
A imagem da curva γ ( t ) está contida na intersecção das superfícies x 2 + y 2 + z 2 = 3 e x 2 + 3 y 2 - z 2 = 3 . Suponha que γ t 0 = ( 1 ,1 ,1 ) e γ ' t 0 ≠ 0 → . Determine a reta tangente a γ em γ
Determine a equação do plano normal, em ( 1 ,2 ,3 ) , à intersecção das superfícies x 2 + y 2 + z 2 = 14 e x y z = 6 .
Determine as equações do plano tangente e da reta normal à superfície dada, no ponto dado. x 2 + 3 y 2 + 4 z 2 = 8 , e m ( 1 , - 1,1 )
Determine um plano que seja tangente à superfície x 2 + 3 y 2 + 2 z 2 = 11 6 e paralelo ao plano x + y + z = 10 .