Exercícios de Vetor Gradiente - Lista de Exercícios Resolvida
Questão 3
Considere as superfícies
Explicite as coordenadas de vetores normais não-nulos e às superfícies e , respectivamente.
Ver solução completaQuestão 5
Considere a superfície de equação . Se o vetor é tangente a em , então:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 7
5) A temperatura, em Kelvin, de certo ambiente é modelada pela função .
(I) Considerando direções unitárias, qual é a maior taxa de resfriamento, ou seja, a taxa de variação mais negativa da temperatura no ponto ?
(II) Uma andorinha move-se na trajetória , onde denota tempo. Qual é a taxa de variação de temperatura sentida pela andorinha quando ela passa pelo ponto ? Dica: Utilize a tangente de no ponto .
(III) O valor encontrado no item (II) é menor (mais negativo) que o encontrado no item (I). Porque isso não contradiz o da taxa de variação no item (I) ser a de maior resfriamento?
Ver solução completaQuestão 9
A temperatura numa câmara cresce com a altura. As isotermas são lâminas horizontais e o módulo do vetor gradiente em cada ponto é diretamente proporcional à altura do ponto. Determine a expressão de em , sabendo-se que é nula quando a altura é zero.
Ver solução completaQuestão 10
Seja , onde e são constantes reais. Que condições devem satisfazer as constantes e para que seja um ponto de mínimo relativo de ? Justifique.
Ver solução completaQuestão 11
3 – Considere a função .
c) Determine os pontos onde o gradiente de se anula.
Ver solução completaQuestão 13
3 – Considere a função .
b) Calcule e desenhe os vetores gradientes nos pontos e . Use o mesmo desenho do item anterior.
Ver solução completaQuestão 14
A curva de nível da função diferenciável é parametrizada por . A curva , tem sua imagem contida no gráfico de .
a) Determine o vetor tangente à curva no ponto .
b) Determine o vetor tangente à curva no ponto .
c) Calcule
Ver solução completaQuestão 15
Diga se cada afirmativa abaixo é verdadeira ou falsa, justificando sua resposta:
- Se duas funções e são tais que é contínua em um determinado valor e é descontínua em , então a composta será descontínua em .
Questão 16
Suponha que em uma certa região do espaço o potencial elétrico V seja dado por
c) Qual a taxa máxima de variação em P (−1, −1, 1)?
Ver solução completaQuestão 17
Determine a curva de nível de
Que seja tangente à curva descrita por
Qual o ponto de tangencia?
Ver solução completaQuestão 19
Considere a função . Calcular o gradiente da função
(a) +
(b) +
(c) +
(d) +
(e) +
Ver solução completaQuestão 20
Seja uma função de classe tal que . Sabendo que exatamente uma das curvas abaixo tem imagem contida na curva de nível de que contém , assinale a alternativa que contém tal curva.
a) .
b) .
c) .
d) .
e) .
Ver solução completaQuestão 21
Seja (ou seja, é positiva) tal que
Onde é um aberto contendo
Calcule e , escrevendo todos os seus cálculos corretamente.
Ver solução completaQuestão 22
Considere a função dada por . Considere a curva de nível de que passa pelo ponto : esta curva tem equação (onde ).
(a) Encontre o valor de .
(b) Escreva uma parametrização para a curva de nível indicando o domínio de .
(c) Escreva um vetor não nulo tangente ao traço de no ponto e um vetor não nulo normal ao traço de no ponto .
Ver solução completaQuestão 23
Considere as superfícies
- Explicite as coordenadas de vetores normais não-nulos e às superfícies e , respectivamente.
Questão 24
Seja a superfície de equação , onde e são constantes. Para que a reta , , seja tangente a no ponto , o valor de deve ser:
- Nenhuma das demais alternativas
Questão 25
A frase: Se é uma função tal que em um ponto e é um vetor unitário, então é .....
Ver solução completaQuestão 26
A temperatura em um ponto é dada por , onde é medida em graus Celsius e em metros. A direção e sentido de maior aumento da temperatura a partir do ponto é dada pelo vetor unitário e a taxa de variação máxima da temperatura neste ponto é ..... graus Celsius por metro.
Ver solução completaQuestão 27
Suponha que em uma certa região do espaço o potencial elétrico seja dado por .
- Em que direção varia mais rapidamente em ?
Questão 28
Questão 4 – Considere a função , onde é uma função diferenciável.
(b) Se , calcule aproximadamente .
Ver solução completaQuestão 29
Questão 4 – Considere a função , onde é uma função diferenciável.
(a) Sabendo que , calcule .
Ver solução completaQuestão 30
A altura do pico do Jabre (município de Matureia – PB) é, de maneira aproximada, dada por
onde mede a altura em relação ao nível do mar e mede as distâncias leste-oeste e norte-sul em relação ao local do pico (medidas em quilômetro). Considerando que você esteja localizado no ponto , determine:
a) A direção de maior declividade para se descer o pico.
Ver solução completaQuestão 31
Seja a função abaixo definida
- Determine o conjunto dos pontos de continuidade de .
- Determine a função gradiente de .
- Determine o conjunto dos pontos onde é diferenciável.
Questão 32
Suponha que em uma certa região do espaço o potencial elétrico V seja dado por
a) Determine a taxa de variação do potencial em P (−1, −1, 1) na direção do vetor
v = 2î − ĵ + 2k .
Ver solução completaQuestão 33
Suponha que representa o valor da temperatura em sobre os pontos do plano .
- Se é um ponto da curva qual o ângulo entre o vetor tangente a em e o vetor gradiente ?
Questão 34
A taxa de variação máxima em e a direção em que isso ocorre é:
- e
- e
- e
- e
Questão 35
Seja a temperatura numa chapa de aço plana. Dado o ponto determine:
c) a taxa de variação da temperatura a partir do ponto na direção de um vetor unitário que faz um ângulo de com o gradiente da temperatura no ponto.
Ver solução completaQuestão 36
Seja a temperatura numa chapa de aço plana. Dado o ponto determine:
b) a direção e sentido a partir do ponto P em que a temperatura aumenta mais rapidamente e a taxa de crescimento da temperatura nessa direção
Ver solução completaQuestão 37
Sem usar o método dos multiplicadores de Lagrange determine os pontos do cone
que estão mais próximos do ponto
Ver solução completaQuestão 38
Considere a curva com e a função . Suponha que e que para todo . Determine:
O gradiente de em .
Ver solução completaQuestão 39
(Capítulo 14.6 – Exercício 51) Mostre que a equação do plano tangente ao elipsoide no ponto pode ser escrita como
Ver solução completaQuestão 40
Questão 1. Calcule as derivadas parciais pela definição, o vetor gradiente, e encontre e para cada uma das funções:
a) .
Ver solução completaQuestão 42
O potencial numa lâmina plana é dado por em volts.
b) Determine a direção e a taxa na qual o potencial eleva-se mais rapidamente no ponto (1,2).
Ver solução completaQuestão 44
Considere uma distribuição de temperatura em uma região do espaço. Uma partícula localziada em precisa esquentar rapidamente. Outra partícula precisa resfriar-se o mais rápido possível. Qual é a taxa máxima de descrescimento da temperatura em .
Ver solução completaQuestão 47
No exercício anterior, calcule o gradiente nos seguintes pontos abaixo.
d)
Ver solução completaQuestão 48
No exercício anterior, calcule o gradiente nos seguintes pontos abaixo.
b)
Ver solução completaQuestão 49
No exercício anterior, calcule o gradiente nos seguintes pontos abaixo.
a)
Ver solução completaQuestão 50
No exercício anterior, calcule o gradiente nos seguintes pontos abaixo.
c)
Ver solução completaQuestão 51
Considere a superfície S dada pela equação . Se o vetor é tangente a em , mostre que .
Ver solução completaQuestão 52
Seja . Identifique e esboce todas as curvas de nível . Para quais valores de temos que a curva de nível correspondente é não vazia?
Ver solução completaQuestão 53
Considere a função .
(a) Indique a direção que determina a maior taxa de crescimento de no ponto . Qual é o valor dessa taxa?
(b) Calcule a derivada direcional de na direção no ponto .
(c) Considere a curva , , e a função composta . Calcule .
Ver solução completaQuestão 54
Seja uma função de classe tal que . Sabendo que exatamente uma das curvas abaixo tem imagem contida na curva de nível de que contém , assinale a alternativa que contém tal curva.
a) .
b) .
c) .
d) .
e) .
Ver solução completaQuestão 55
Seja uma função de classe tal que . Sabendo que exatamente uma das curvas abaixo tem imagem contida na curva de nível de que contém , assinale a alternativa que contém tal curva.
a) .
b) .
c) .
d) .
e) .
Ver solução completaQuestão 58
2.1. Se , ache o vetor gradiente e use-o para achar a reta tangente à curva de nível de no ponto . Esboce a curva de nível, a reta tangente e o vetor gradiente.
Ver solução completaQuestão 59
2.4. Considere uma função de classe . Suponha que:
(i) a imagem da curva plana , para , esteja contida numa curva de nível de .
(ii) a imagem da curva no espaço , com , esteja contida no gráfico de .
a. Determine
Ver solução completaQuestão 60
Encontre as equações dos planos tangentes ao gráfico de que passam por ambos os pontos e
Ver solução completaQuestão 61
Um reservatório cilíndrico fechado deve conter litros de fluido, onde é o número formado pelos últimos três dígitos do seu RA. Determine as dimensões do depósito de modo que a quantidade de material usada em sua construção seja mínima e determine qual é a área mínima.
Ver solução completaQuestão 62
- Afigura mostra uma porção de um mapa da região Sul de Minas Gerais onde estão indicadas as curvas de nível da função altura com relação ao nível do mar. Existe uma linha grossa para cada de elevação e uma linha fina em cada intervalo de . Considere os pontos e no mapa. As setas indicam o vetor gradiente de no ponto indicado. Diga se as relações abaixo são verdadeiras ou não, marcando um “V” se a relação for verdadeira ou um “F” se a relação for falsa.
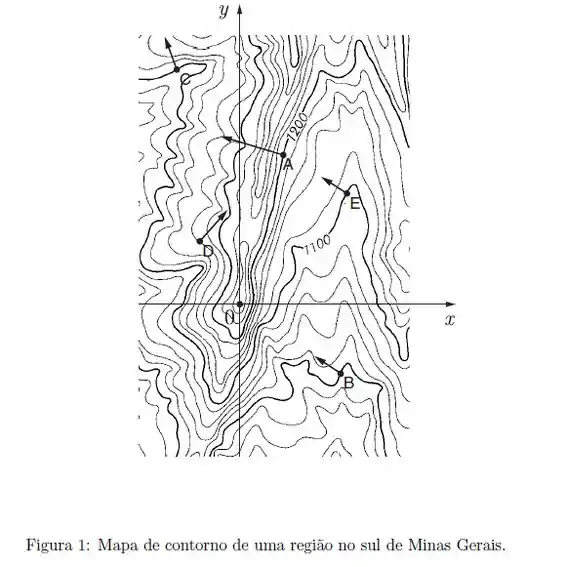
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
Ver solução completaQuestão 64
A temperatura é medido em graus em qualquer ponto da placa retangular situado no plano e . A distância é medida em metros. Assinale a alternativa correta que determine a taxa de variação máxima no ponto e a direção e sentido em que a taxa de variação é máxima em .
a taxa de variação correspondente a e a taxa máxima de ocorre na direção e sentido do
a taxa de variação correspondente a e a taxa máxima de ocorre na direção e sentido do
a taxa de variação correspondente a e a taxa máxima de ocorre na direção e sentido da derivada direcional
a taxa de variação correspondente a e a taxa máxima de ocorre na direção e sentido do
Ver solução completaQuestão 66
Seja uma função de classe tal que . Sabendo que exatamente uma das curvas abaixo tem imagem contida na curva de nível de que contém , assinale a alternativa que contém tal curva.
a) .
b) .
c) .
d) .
e) .
Ver solução completaQuestão 67
Considere a função
(a) Calcule e explique as suas discrepâncias geométricas.
(b) Encontre a taxa máxima de variação da função no ponto . Determine a direção em que essa taxa máxima de variação ocorre.
(c) Encontre a equação do plano tangente ao gráfico de no ponto .
(d) Encontre a linearização de em , use-a para calcular aproximadamente e explique por que é possível usar a sua linearização para aproximar .
Ver solução completaQuestão 68
A temperatura é medido em graus em qualquer ponto da placa retangular situado no plano e . A distância é medida em metros. Assinale a alternativa correta que determine a taxa de variação máxima no ponto e a direção e sentido em que a taxa de variação é máxima em .
a taxa de variação correspondente a e a taxa máxima de ocorre na direção e sentido do
a taxa de variação correspondente a e a taxa máxima de ocorre na direção e sentido do
a taxa de variação correspondente a e a taxa máxima de ocorre na direção e sentido da derivada direcional
a taxa de variação correspondente a e a taxa máxima de ocorre na direção e sentido do
Ver solução completaQuestão 69
7. As curvas definidas a seguir se interceptam no ponto , formando um ângulo de rad.
e
a) Encontre um valor possível para . Quantas soluções tem esse problema?
b) Resolva o mesmo problema supondo que o ângulo é rad.
Sugestão: Nos dois casos encontre um vetor perpendicular a curva em , um vetor tangente a curva em e use a fórmula do ângulo entre esses vetores,
Ver solução completaQuestão 72
26 Considere a função cuja lei é dada por .
(a) Encontre a aproximação linear de para no ponto .
Ver solução completaQuestão 73
Considere uma função de classe . Suponha que:
- A imagem da curva plana , para t esteja contida numa curva de nível de f,
- A imagem da curva no espaço com , esteja contida no gráfico de f.
b. Calcule onde
Ver solução completaQuestão 74
Suponha que em uma certa região do espaço o potencial elétrico seja dado por .
- Qual a taxa de variação máxima em ?
Questão 75
Sejam uma função diferenciável e , uma curva cuja imagem está contida no gráfico f. Seja r a reta tangente à curva de nível 4 de f no ponto . Sabendo que a reta r contém o ponto determine o vetor gradiente de f no ponto e a equação de plano tangente ao gráfico de f no ponto
Ver solução completa