Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 6.4 - Ex. 11
Sejam e como no Exercício 10. Prove que
Área de
Passo 1
Pelo Exercício 10, temos: Consideremos funções de classe tais que , . E ainda seja nosso
Ou seja,
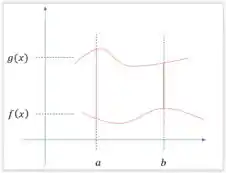
Assim faremos o seguinte
Passo 2
Uma maneira fácil de resolvermos nosso problema é aplicarmos o que vimos anteriormente nos exercício 10. Desta forma fazemos o seguinte
Mostrando que nosso exercício era mais simples do que realmente parecia ser.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use o Use o teorema de Green para calcular ∫ C F → ⋅ d r → . (Verifique a orientação da curva antes de aplicar o teorema.)
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . y d x - x d y C é uma circunferência com centro na origem e r a i o = 4 .
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x y d x + x 2 y 3 d y C é um triângulo com os vértices em 0,0 , 1,0e( 1,2 ) .
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y e x d x + 2 e x d y C é um retângulo com os vértices 0,0 , 3,0 , 3,4e( 0,4 ) .
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o