Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 11
Use o teorema de Green para calcular . (Verifique a orientação da curva antes de aplicar o teorema.)
Onde, é o triangulo de
Passo 1
E aii galera, belezinha? Vamos nessa então!
Precisamos usar o teorema de Green para calcular a integral de linha:
Onde,
E é o triangulo de
Mas antes verifique a orientação da curva.
Bom, o primeiro passo é desenhar esse triângulo e verificar a orientação. Fazendo isso temos:
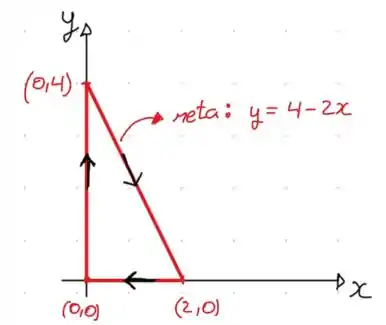
Ao representar o triangulo seguindo o caminho indicado pelos vértices temos uma curva no sentido horário.
O Teorema de Green tem a seguinte cara e ele é valido para curvas no sentido anti-horário:
Mas a gente pode usar o teorema de Green se adotarmos o caminho com sentido negativo, dessa forma:
Observe também que podemos assumir as seguintes variações dos limites de integração:
Agora ficou moleza ein, só colocar mão na massa!
Vamos lá!!!
Passo 2
Já identificamos que a questão está orientando a curva no sentido horário, e para aplicar o Teorema de Green devemos fazer a correção com o sinal negativo.
Ficando com a seguinte expressão:
Dado um campo , podemos identificar o P e Q da seguinte forma:
Comparando:
Temos que:
Aplicando então o teorema de Green, ficamos com:
Lembrando que nossa região é delimitada por:
Lembre-se, que sempre começamos integrando pelo termo que possui função nos limites de integração.
Passo 3
Voltando para nossa integral. E aplicando as derivadas em relação a e , vamos ter:
Simplificando, temos:
Substituindo os limites de integração, vamos ter:
Integrando primeiro em , temos:
Aplicando os limites de integração, ficamos com:
Por fim, integrando em vamos ter:
Aplicando os limites de integração, vamos ter:
Logo, concluímos que pelo teorema de Green a resposta é: