Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.3 - Ex. 24
Lembrando que é definido como
E é a função escada definida por
Ache, se existirem:
Passo 1
Vamos começar fazendo um esboço de . Para isso temos que entender um pouquinho só como é essa nossa
O enunciado disse que
Pegando a definição dessa função e a de conseguimos achar o
Para isso, vamos pegar a e ir subtraindo o valor de
Vamos olhar com calma cada intervalo da função .
Primeiro em : O valor de vai ser
Agora em : O valor de vai ser
Agora em : O valor de vai ser
Então, vai ser
Arrumando isso, vamos ter
Então ela vai ser até o , incluindo o . Isso faz com que se tenha que colocar uma bolinha fechada em e .
Depois ela vai ser para valores maiores que . Lembrando de colocar a bolinha aberta em
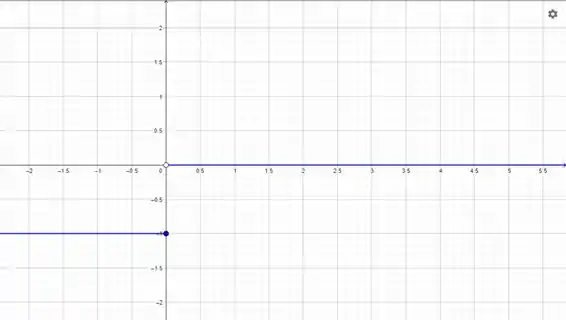
Passo 2
Letra
Agora vamos aos limites que ele pediu
Aqui, temos que ver o comportamento da função quando se aproxima de pela direita. Que é se aproximar de por valores maiores que .
Olhando o gráfico, chegando perto de pela direita, a nossa função se aproxima de .
Mesmo que ela de fato seja em , a reta azul chega muuuuuito perto de na verdade.
Passo 3
Letra
Agora o outro
Aqui, temos que ver o comportamento da função quando se aproxima de pela esquerda. Que é se aproximar de por valores menores que .
Olhando o gráfico, chegando perto de pela esquerda, a nossa função se aproxima de .
Mesmo que ela de fato seja em , a reta azul chega muuuuuito perto de na verdade.
Passo 4
Letra
Para o limite que ele pediu, temos que comparar os limites laterais.
Se eles forem iguais, o limite em vai existir e será esse valor. Se eles forem diferentes o limite não existe.
Pelas letras e , os dois limites laterais vão ser e , respectivamente.
Eles são diferentes, então o limite não existe.
Resposta
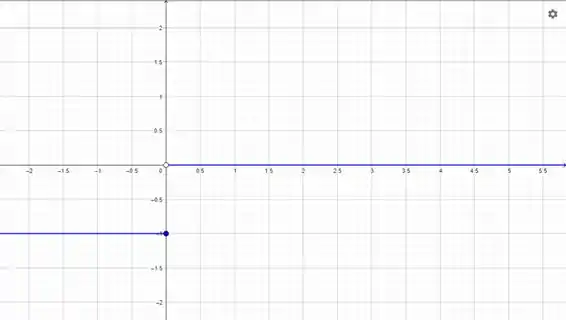
Não existe o limite