Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.4 - Ex. 31

Suponha que f seja lisa em [ a , b ] e dividida [ a , b ] da maneira usual. No k - é s i m o subintervalo [ x k - 1 ,   x k ] , construa a reta tangente à curva no ponto médio m k = x k - 1 + x k 2 , como mostra a figura a seguir.

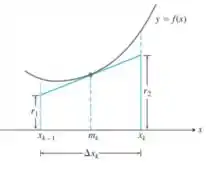
  1. Demonstre que

    2. r 1 = f m k - f ' m k ∆ x k 2                 e                     r 2 = f m k + f ' m k ∆ x k 2 .

  2. Mostre que o comprimento L k do segmento de reta tangente no k - é s i m o subintervalo é L k = ∆ x k 2 + f ' m k   ∆ x k 2 .
  3. Demosntre que a área da superfície lateral do tronco de cone gerado pelo segmento de reta tangente, ao girar em torno do eixo x , é 2 π   f m k 1 + f ' m k 2   ∆ x k .
  4. Demosntre que a área da superfície gerada pela rotação de y = f ( x ) em torno do eixo x em [ a , b ] é de

∑ k = 1 n ( á r e a   d a   s u p e r f í c i e   l a t e r a l   d o   k - é s i m o   t r o n c o )         =   ∫ a b 2 π f x 1 + f ' x 2 d x   .  

Passo 1

  1. A equação da reta tangente é dada por y = f m k + f ' m k x - m k .

    2. Quando x = x k - 1 , nós temos :

    y = r 1 = f m k + f ' m k x k - 1 - m k = f m k + f ' m k - ∆ x k 2 = f m k - f ' m k ∆ x k 2

    Quando x = x k , nós temos:

    y = r 2 =   f m k + f ' m k x k - m k = f m k + f ' m k ∆ x k 2

    Passo 2

  2. Pelo Teorema de Pitágoras podemos escrever que:

    3. L k 2 = ∆ x k 2 + r 2 - r 1 2 = ∆ x k 2 + f ' m k ∆ x k 2 - - f ' m k ∆ x k 2 2 =

    = ∆ x k 2 + f ' m k ∆ x k 2 ⇒ L k = ∆ x k 2 + f ' m k ∆ x k 2

    Passo 3

  3. Pela geometria temos que a área da superfície lateral do tronco de cone gerado pelo segmento de reta tangente, ao girar em torno do eixo x , é

    4. ∆ S k = π r 1 + r 2 L k = π 2 f m k ∆ x k 2 + f ' m k ∆ x k 2

    Utilizando as respostas obtidas em a e   ( b ) , temos que:

    ∆ S k = 2 π f m k 1 + f ' m k 2     ∆ x k .

    Passo 4

S = ∑ k = 1 n ∆ S k =   ∑ k = 1 n 2 π f m k 1 + f ' m k 2     ∆ x k =        

= ∫ a b 2 π f x 1 + [ f ' ( m k ) ] 2   d x

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado. y = x + 1 ,1 ≤ x ≤ 5 ;e i x ox
Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado. x = y 3 3 , 0 ≤ y ≤ 1 ; e i x oy
Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado.Se você tiver um programa gráfico, poderá traçar o gráfico da curva para verificar a sua aparência. x = 1 3 y 3 2
Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado. x = 2 4 - y , 0 ≤ y ≤ 15 4 ; e i x oy
Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado. x = 2 y - 1 ,5 8 ≤ y ≤ 1 ; e i x oy