Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 14
Trace a curva e calcule a área delimitada por ela.
Passo 1
Fala pessoal. Partiu resolver uma questão de área?
A questão pede para traçar a curva descrita pela equação polar e calcular a área delimitada por ela. Para resolver, os procedimentos a serem seguidos são:
- Para traçar a curva polar temos que calcular os valores de para diferentes valores de e plotar esses pontos em um gráfico polar. Isso nos permitirá visualizar a forma da curva e principalmente o limites de integração.
- Usaremos a fórmula da área em coordenadas polares,
- Por fim vamos integrar a expressão e aplicar os limites de integração para encontrar a área.
onde o intervalo de integração são os ângulos de início e fim da curva.
Vamos começar?
Passo 2
Vamos começar traçando o gráfico da curva. Para isso, vamos plotar alguns pontos usando valores específicos de e calcular seus respectivos .
E assim por diante, até , onde voltamos ao ponto inicial. Sendo assim, o gráfico de é representado pela seguinte curva:
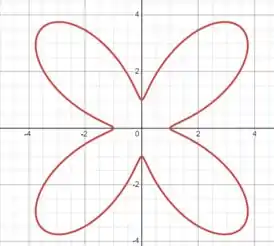
Passo 3
Vamos verificar os limites de integração a partir do gráfico?
Se liga! A linha que forma a fronteira do gráfico começa em e da uma volta inteira, ou seja, percorreu um ângulo , o que representa uma volta completa.
Assim, quando calculamos a área delimitada por uma curva em coordenadas polares, integramos em relação a de a , cobrindo todo o domínio angular da curva.
Passo 4
Aplicando os limites de integração e substituindo , obtemos:
Resolvendo o produto notável, temos
Podemos usar a propriedade trigonométrica:
Aplicando o método da multiplicação distribuitiva no último termo
Passo 5
Resolvendo a integral em cada termo, obtemos
Aplicando o limite de integração