Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.2 - Ex. 78
Trace as curvas ,, para na mesma tela. Encontrando as áreas entre as curvas sucessivas, dê uma demonstração geométrica do fato, mostrado no Exemplo 6, de que
Passo 1
Fala aí, meus amores!
Primeira coisa que o enunciado nos perde é pra traçar os gráficos de ,, para Em outras palavras, os gráficos de:
Todas essas funções passam pela origem. A primeira é uma reta de inclinação 1. A segunda é uma parábola. A terceira, é uma função de terceiro grau e por aí vai. O comportamento dessas funções já é bem típico e conhecido, na literatura. Então olha como elas ficam:
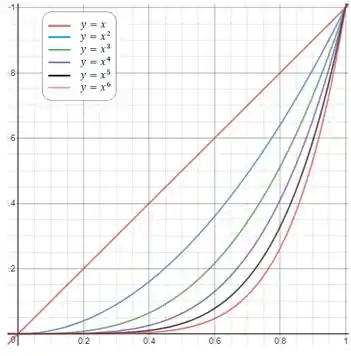
Podemos ver pelo gráfico que com, a medida que aumenta, a curva fica abaixo da anterior, então podemos dizer que a área entre duas curvas consecutivas é
Os limites de integração são dados pelo domínio que o enunciado estabelece.
E sabemos que se somarmos todas as áreas de até , vamos chegar a área abaixo da primeira curva.
Vamos calcular essas integrais e substituir aqui.
Passo 2
Pra calcular as integrais, como são só integrais de polinômio, basta usar
Vamos lá, como são integrais definidas, não temos a constante de integração
Passo 3
Como definimos no passo 1:
Substituindo o que achamos no passo 2:
Vamos trabalhar com o termo da série
Fazendo MMC
Substituindo na série
Agora vamos manipular mais um pouco!
Passo 4
Como queremos o termo , vamos substituir , ou na série
Mas a série do enunciado começa com o índice , então vamos ter que somar esse primeiro termo do outro lado para igualar
Quando o termo vale , então
Podemos substituir por que não vai fazer diferença, mas chegamos no que ele queria.
Resposta
Demonstração.