Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.4 - Ex. 54

Trace a função y = 1 // ( x^3 - 2 x^2 ) e sua primitiva na mesma tela.

Passo 1

Devemos encontrar a primitiva para a função e traçar ambos as curvas no mesmo gráfico. Para encontrar a primitiva da função, vamos recorrer às frações parciais.

(1)/(x^3 - 2 x^2) = (1)/(x^2 (x - 2)) = (A)/(x) + (B)/(x^2) + (C)/(x - 2)

Portanto,

A x (x - 2) + B (x - 2) + C x^2 = 1

Logo,

(A + C) x^2 + (- 2 A - 2 B) x - 2 B = 1

Desta forma, B = - 1 // 2 e, como - 2 A - 2 B = 0 => A = - B = 1 // 2 . Além disso, A + C = 0 => C = - A = - 1 // 2 . Assim,

int (1)/(x^3 - 2 x^2) d x = (1)/(2) int ((1)/(x) - (1)/(x^2) - (1)/(x - 2)) d x

Passo 2

Calculando a integral e fazendo a constante de integração igual a 0 , temos que

int (1)/(x^3 - 2 x^2) d x = (1)/(2) ln | x | + (1)/(2 x) - (1)/(2) ln | x - 2 |

Passo 3

Em vermelho traçamos o gráfico da função e em azul sua primitiva:

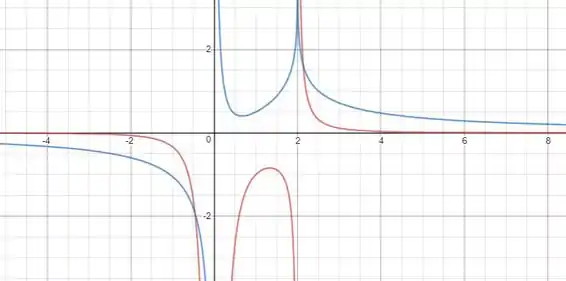
Resposta

Esboço de gráfico.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as integrais. Talvez seja necessário fazer substituição primeiro.
Calcule a integral ∫ 0 1 x 3 + 2 x x 4 + 4 x 2 + 3 d x
Calcule a integral int_0^1 (x - 4)/(x^2 + 5 x + 6) d x
Calcule a integral ∫ 4 x x 3 + x 2 + x + 1 d x
Calcule a integral int (a x)/(x^2 - b x) d x