Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 87
Um triângulo isósceles tem seu vértice na origem, e sua base é paralela ao eixo x, estando os vértices da base acima do eixo, sobre a curva . Determine a maior área que o triângulo pode assumir.
Passo 1
A partir dos dados do enunciado, podemos construir o seguinte gráfico:
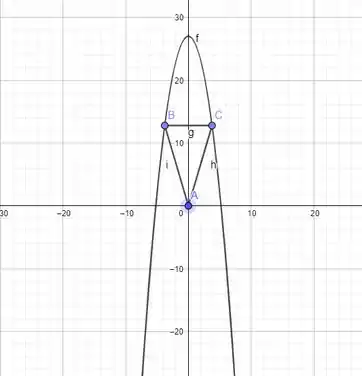
A base do triângulo pertence a uma reta qualquer . E a interseção dessa reta com a curva se dá nos pontos B e C. Tendo as coordenadas dos pontos B e C em função de k, podemos calcular a expressão para a área em função de k. A fim de maximizar essa expressão, iremos derivar e igualar a zero.
Passo 2
Encontrando as coordenadas dos pontos B e C:
Como B está no segundo quadrante (x0), podemos inferir que:
Portanto, temos as coordenadas dos vértices do triângulo:
A: (0,0)
B:
C:
Passo 3
Vamos agora calcular a área A do triângulo:
Onde a base b é o segmento BC e a altura h é . O segmento BC vale .
Logo,
Vamos agora derivar a expressão da área e igualar a zero. Pela regra do produto, temos:
Substituindo o valor de k encontrado na expressão da área, temos:
Resposta
A maior área que o triângulo pode possuir é de 54 u.a.