Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 31
Use coordenadas esféricas.
- Encontre o centroide do sólido do Exemplo 4 (assuma densidade constante ).
- Encontre o momento de inércia ao redor do eixo para esse sólido.
Passo 1
Fala, galerinha! Tudo joia?
Nossa questão tem duas partes sobre o Exemplo 4: sólido que fica entre o cone e abaixo da esfera .
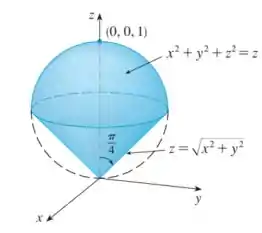
A parte a) pede o centroide desse sólido, que a gente pode achar usando a equação:
Onde é:
E os momentos em torno de cada eixo:
A parte b) quer o momento de inércia em torno do eixo , que podemos achar através de:
Passo 2
- Encontre o centróide do sólido do Exemplo 4 (assuma densidade constante )
- Encontre o momento de inércia ao redor do eixo para esse sólido.
Olhando o sólido do Exemplo 4, podemos facilitar nossa vida ao perceber que a superfície é simétrica co relação aos eixos e , e, dessa forma, temos:
Temos que a massa do sólido é dada por:
Como é constante, podemos tira-la para fora da integral, ficanco com:
E, o próprio Exemplo 4 já nos fornece o valor da integral do volume do sólido, que é , então, substituindo esse valor na equação da massa, temos:
Passo 3
Agora devemos calcular o momento de massa com relação ao eixo do sólido, para isso, fazemos:
Através dos limites de integração fornecidos no exemplo 4, podemos reescrever a integral como:
Resolveremos essa integral de maneira iterada, começando por , temos:
Simplificando, obtemos:
Agora, separando as integrais em função de suas variáveis, podemos escrever:
Passo 4
Antes de resolver a integral, devemos notar que, para , devemos aplicar uma integral por substituição. Sabemos que as integrais com formato:
São resolvidas por substituição, fazendo e a integral se torna:
Nesse caso, temos , então, resolvendo a integral em , temos:
Resolvendo para as duas variáveis simultaneamente, temos:
Dessa forma, o centróide é dado por:
Passo 5
Nós sabemos que o momento de inércia ao redor do eixo será dado por:
Das equações de transformação para coordenadas esféricas, temos:
Substituindo as relações de transformação na equação anterior e aplicando os intervalos de integração vistos no exemplo 4, temos:
Da relação fundamental da trigonometria, temos , e podemos simplificar a integral para:
Resolvendo essa integral de maneira iterada começando por , temos:
Simplificando, obtemos:
Passo 3
Agora iremos usar a relação trigonométrica para reescrever a integral acima:
E, simplificando, temos:
Agora, separando as integrais em função de suas variáveis, podemos escrever:
Antes de resolver a integral, devemos notar que, para , devemos aplicar uma integral por substituição. Sabemos que as integrais com formato:
São resolvidas por substituição, fazendo e a integral se torna:
Nesse caso, temos e , então, resolvendo a integral em , temos:
Resolvendo para as duas variáveis simultaneamente, temos: