Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 64

Use a geometria ou simetria, ou ambas, para calcular a integral dupla

∬ D R 2 - x 2 - y 2 d A

D é o disco com centro na origem e raio R.

Passo 1

Fala pessoal, tudo bem com vocês? Bora resolve mais uma!

A questão forneceu a seguinte integral dupla:

∬ D R 2 - x 2 - y 2 d A

Onde a região D é o disco com centro na origem e raio R .

A partir disso, devemos calcular o valor dessa integral usando a geometria ou simetria, ou ambas.

Vish, como resolvo essa?

Vamos pensar juntos!

Esse tipo de questão é interessante pois nos cobra o uso de propriedades (quando falamos de simetria estamos pensando na paridade de funções) ou na comparação do sólido com o volume de uma figura.

Sabemos que o volume é definido por:

V = ∬ D z d A

Observe a função:

z = z ( x , y ) = R 2 - x 2 - y 2

Repare que se igualarmos tudo a R 2 , vamos ter uma esfera completa certo. Mas nossa função não é uma esfera completa, porque temos a raiz quadrada de: R 2 - x 2 - y 2 .

Como temos a raiz quadrada, função é positiva independentemente dos valores de x e y . Dessa forma concluímos que estamos avaliando somente a parte positiva de z , ou seja, uma semiesfera cujo centro é a origem O = 0,0 , 0 e possui raio R .

Com essa análise, sabemos que o volume vai ser metade do volume de uma esfera de raio R.

V = ∬ D R 2 - x 2 - y 2 d A = 1 2 V e s f e r a

V e s f e r a = 4 3 π R 3

Sabendo disso, esboce as regiões para facilitar o entendimento.

Vamos nessa!!

Passo 2

Vamos começar esboçando as regiões.

Lembra que falamos que isolando R 2 na função de z , iriamos encontrar uma esfera. Vamos verificar isso.

z = R 2 - x 2 - y 2

z 2 = R 2 - x 2 - y 2

Isolando R 2 , temos:

z 2 + x 2 + y 2 = R 2

Antes vamos assumir um raio R = 1 , para podermos fazer o gráfico. Logo utilizando o Geogebra, temos:

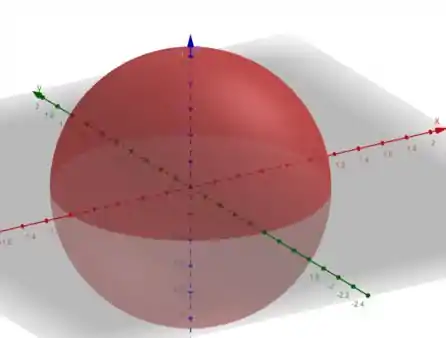
Comprovamos que realmente é uma esfera.

Passo 3

Agora observe o gráfico em função de z , também assumindo R = 1 .

z = 1 2 - x 2 - y 2

Com o auxílio do Geogebra, temos:

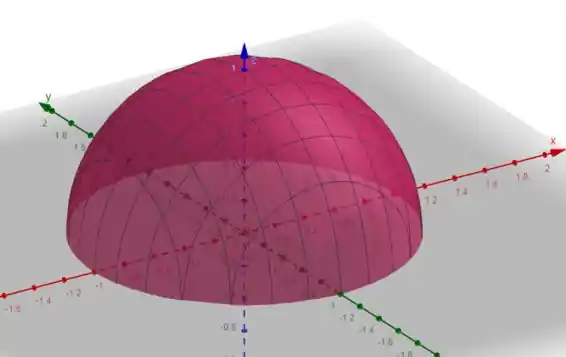
Observe que obtemos uma semiesfera, somente com valores de z positivo. E isso ocorre devido a raiz quadrada.

Então quem é nossa região D ? Para determinar, igualamos z = 0 . Vamos ter:

R 2 - x 2 - y 2 = 0

Simplificando, temos:

x 2 + y 2 = R 2

Um disco no plano x y :

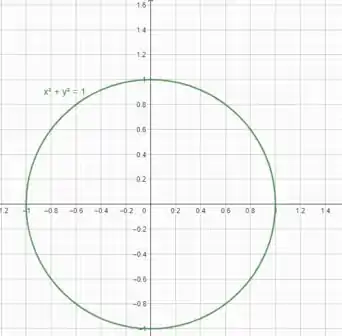
Portanto, precisamos obter o volume acima da região D no plano x y e abaixo da superfície da esfera.

Como queremos obter o volume de toda uma semiesfera! Por simetria, sabemos que vai ser a metade do volume de uma esfera de raio R .

V = 1 2 V e s f e r a

V e s f e r a = 4 3 π R 3

Portanto, o resultado da nossa integral é:

∬ D R 2 - x 2 - y 2 d A = 1 2 4 π R 3 3 = 2 π R 3 3

Resposta

∬ D R 2 - x 2 - y 2 d A = 2 π R 3 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma carga elétrica é distribuída sobre um disco x 2 + y 2 ≤ 4 de modo que a densidade de carga em x ,y é σ x ,y = x + y + x 2 + y 2 (medida em coulombs por metro quadrado). Determine a carga total no
Uma carga elétrica é distribuída sobre o retângulo 1 ≤ x ≤ 3, 0 ≤ y ≤ 2, de modo que a densidade de carga em x ,y é σ x ,y = 2 x y + y 2 (medida em coulombs por metro quadrado). Determine a carga tota
Determine o volume do sólido dado.Limitada pelos cilindros z = x 2 , y = x 2 e pelos planos z = 0 , y = 4
Determine o volume do sólido dado.Limitada pelos planos z = x , y = x , x + y = 2 e z = 0
Determine o volume do sólido dado.Limitada pelo cilindro y 2 + z 2 = 4 e pelos planos x = 2 y , x = 0 , z = 0 no primeiro octante