Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 30
Determine o volume do sólido dado.
Limitada pelo cilindro e pelos planos , , no primeiro octante
Passo 1
Faala, galera!
Essa questão a gente precisa calcular o volume de um sólido...
Vamos lembrar que a gente consegue calcular o volume de um sólido abaixo do gráfico de uma função sobre uma região com uma integral:
Então pra calcularmos o volume desse sólido a gente vai ter que encontrar quem é esse e quem é a região .
Sabendo quem é e , vamos calcular a integral, e achamos o volume!
Passo 2
Podemos começar com um esboço das superfícies que limitam nosso sólido:
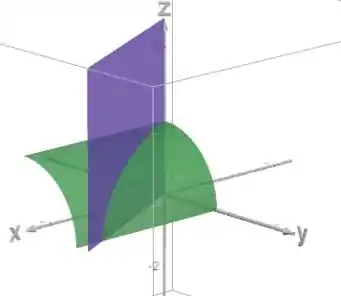
A superfície verde é o cilindro , restrito ao primeiro octante.
O plano roxo é .
O plano é o plano , e o plano é o plano .
O sólido que queremos achar o volume é a região embaixo do gráfico da função que define o cilindro. Os planos vão delimitar o domínio .
Então primeiro vamos achar a função , isolando o na expressão do cilindro :
Como estamos falando do primeiro octante, , então
Então o volume é:
Falta encontrar quem é .
Passo 3
Pra achar a região , vamos olhar as interseções das superfícies no plano :
Os planos , e viram retas.
O cilindro , como nesse plano , fica:
Mas estamos no primeiro octante (), então:
No plano , essas retas definem a região de integração :
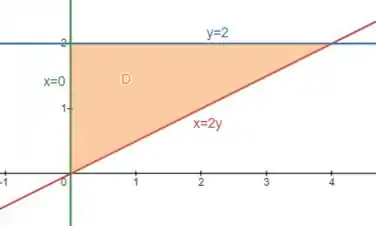
Então, podemos escrever como uma região do tipo II da seguinte forma
Passo 4
Temos então que o volume do solido que é restrito abaixo de na região é dado por
Agora vamos integrar, primeiro em , mantendo constante?
Agora em relação a , vamos usar a substituição
Mudando os limites de integração
Substituindo
Como temos um menos antes da integral, podemos inverter os limites
Então: