Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 25
Use a Regra do Ponto Médio para as integrais triplas (Exercício 24) para estimar o valor da integral. Divida em oito subcaixas de tamanho igual.
Onde .
Passo 1
Faaala, pessoal!
Nessa questão precisamos estimar o valor de uma integral usando a Regra do Ponto Médio.
Vamos relembrar essa regra, que é uma forma de aplicarmos a soma de Riemann:
Onde os pontos amostrais que usamos para calcular a soma são os pontos médios de cada partição:
Nessa questão, vamos dividir nosso sólido em oito partes iguais, ou seja, dividimos em cada um dos eixos ( e ) em duas partes ():
Vamos começar desenhando nosso sólido e definindo as subcaixas e os pontos médios.
Depois, vamos fazer as contas!
Passo 2
O sólido é um cubo de aresta :
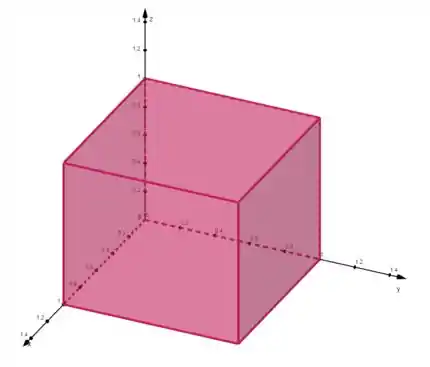
Vamos dividir esse cubo em oito partições iguais. Percebe que cada partição é também um cubo, com aresta medindo metade da aresta do cubo inteiro () – isso porque dividimos em duas partições em cada eixo!
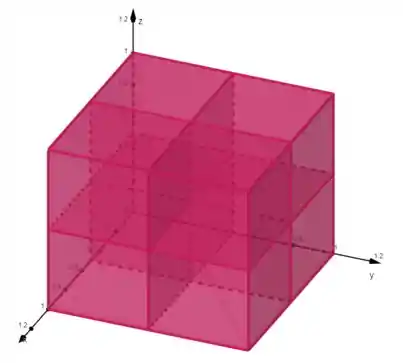
Vamos marcar os pontos médios de cada partição. Eles são os pontos exatamente no centro de cada cubo:
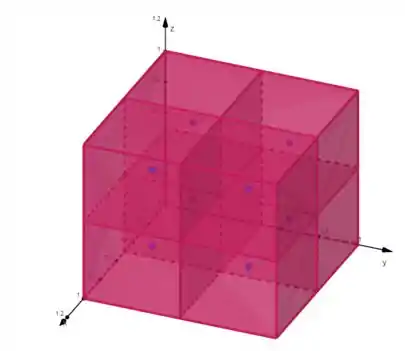
Esses pontos são:
Além disso, vamos calcular o volume das partições.
Como já vimos, elas são cubos de aresta , então:
Passo 3
Agora, vamos fazer as contas!
Como o é constante, ele pode sair do somatório:
Como nossa função é , para cada partição vamos calcular:
Depois vamos somar tudo e multiplicar essa soma por .
Para o ponto :
Para os pontos :
Para os pontos :
Para o ponto :
Somando tudo:
Fazendo essa conta na calculadora encontramos: