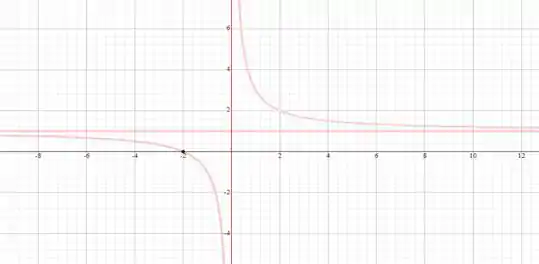
Use o roteiro desta seção para esboçar a curva:
Passo 1
Fala, galera! Beleza? O enunciado pediu pra gente esboçar o gráfico da função
usando o roteiro da seção onde a questão se encontra.
Para isso, vamos ter que seguir os seguintes passos:
- Definir o domínio de .
- Determinar as interseções da curva com os eixos e
- Verificar se a função possui simetrias.
- Verificar se a função possui assíntotas.
- Calcular e usar o Teste C/D para definir os intervalos de crescimento e decrescimento de .
- Encontrar os números críticos de e usar o Teste da Primeira Derivada para encontrar os pontos e valores de máximo e mínimo de .
- Calcular e usar o Teste da Concavidade para verificar onde a curva é côncava para cima ou para baixo e os seus pontos de inflexão.
Vamos resolver essa questão com calma, combinado? Quando tivermos todas as informações, vamos esboçar o gráfico da função
Bora lá! 😊
Passo 2
- Definir o domínio de .
💡 Lembrando:
- O domínio de é o conjunto dos valores de para os quais está definida.
A função
é um quociente, então não está definida para valores em que o denominador é zero. Vamos descobrir que valores são esses!
Como
então
quando
Assim, o domínio da função é:
Passo 3
💡 Lembrando:
- Para descobrir a interseção com o eixo , precisamos avaliar a função em .
- Para descobrir a interseção com o eixo , precisamos avaliar a função em .
Como vimos no passo anterior que a função não está definida em então a função não intersecta o eixo
Além disso, como
e
então substituindo em
teremos:
Podemos simplificar o fator .
Assim:
logo,
Isso mostra que é o ponto de interseção da curva com o eixo .
Passo 4
💡 Lembrando:
- Se para todo em , é uma função par e a curva é simétrica em relação ao eixo .
- Se para todo em , é uma função ímpar e é simétrica em relação à origem.
- Se para todo em , onde é uma constante positiva, é uma função periódica e o menor desses números é chamado de período.
Podemos verificar que não possui simetria, avaliando em , por exemplo.
- A função não é par. Pois:
- A função não é ímpar. Pois:
- Não possui período.
e
Ou seja,
e
Ou seja,
Como não satisfaz nenhum dos casos, não possui simetria.
Passo 5
💡 Lembrando:
- Para assíntotas horizontais: Calcular os limites de para mais ou menos infinito. Se esse resultado for um valor constante, então esse valor será uma assíntota horizontal da função.
- Para assíntotas verticais: Como a função é racional, vamos calcular o limite para os pontos que zeram o denominador, encontrados no Passo 2.
Como (dividindo pelo termo de maior potência)
e simplificando o fator então:
Calculando o limite do numerador e do denominador, temos que
A função tem uma assíntota horizontal em .
Agora vamos verificar se existem assíntotas verticais.
Para , vamos verificar se existe uma assíntota vertical.
Calculando o limite de tendendo para
Simplificando:
ou seja:
Como esse limite explode pra infinito, a função uma assíntota vertical em .
Da mesma forma, para :
Logo, não é uma assíntota vertical.
Passo 6
💡 Lembrando:
- Se em um intervalo, então é crescente nele.
- Se em um intervalo, então é decrescente nele.
- Encontrar os números críticos de e usar o Teste da Primeira Derivada para encontrar os pontos e valores de máximo e mínimo de .
- Um número crítico de é um ponto em que ou não existe!
- Se muda de positiva para negativa em um número crítico , então é um máximo local.
- Se muda de negativa para positiva em , então é um mínimo local.
Aplicando a regra do quociente para derivadas em (simplificação vista no Passo 3).
Para todo
Logo, é decrescente em todo o domínio D.
Passo 7
💡 Lembrando:
Teste da Primeira Derivada:
Assim, como
a derivada nunca é igual a zero para nenhum valor real.
Perceba que apesar de ser um ponto onde a derivada não está definida, como ele não está no domínio da função , ele não pode ser um número crítico de .
A função não possui pontos extremos.
Passo 7
💡 Lembrando:
- Se , a função é côncava para cima.
- Se , a função é côncava para baixo.
Como
então é côncava para baixo com no intervalo e côncava para cima com nos intervalos e .
Se quiser confirmar, pegue um ponto dentro do intervalo e avalie a função neste ponto.
Passo 8
Use as informações que descobrimos nos passos anteriores para marcar os pontos de máximo e mínimo, e esboçar a curva considerando a concavidade e o sinal da função em cada intervalo que achamos. 😊
Em seguida, compare com o gráfico dado.
Vamos resumir as informações importantes aqui.
- O domínio da função é
- A função não intersecta o eixo e só tem um ponto de interseção com o eixo , que é o ponto
- A função não possui nenhuma simetria nem período.
- A função tem uma assíntota horizontal e uma assíntota vertical
- A função é decrescente em todo o domínio, ou seja, em , e
- A função não possui extremos.
- A função tem concavidade para baixo no intervalo e concavidade para cima nos intervalos e
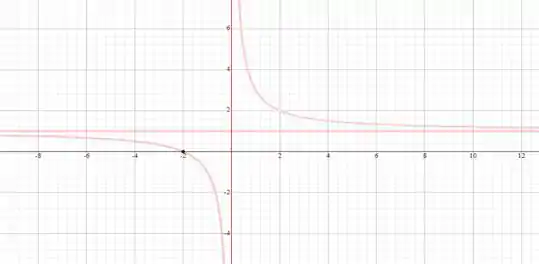
Ufa! Conseguimos. Até a próxima 😊!
Resposta