Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 36
Use um sistema de computação algébrica para achar o volume exato do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno da reta especificada.
Passo 1
Bom galera, antes de começar vamos desenhar a situação:
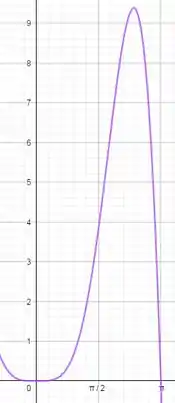
Então, nós queremos o volume formado pela rotação da área formada entre estas duas funções.
E como fica o volume usando o método das cascas cilíndricas nestes casos?
Ficou fácil, não? Basta substituirmos porque já temos tudo o que precisamos:
Tiramos as constantes:
Usando um sistema de computação algébrica:
Resposta
Exercícios de Livros Relacionados
Resolva o Exercício 16, se os dois planos estiverem em lados diferentes opostos em relação ao centro da esfera, mas todos os demais permanecem os mesmos.
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados
Ache o volume do sólido gerado pela rotação da região limitada pela curva de y = | x - 2 | , pelo eixo x , e pelas retas x = 1 e x = 4 , em torno do eixo x .
Use integração para encontrar o volume de sum segmento de uma esfera, se ela tiver um raio de r unidades e se a altura do segmento for h unidades.
A base do sólido é a região encerrada por um círculo tendo um raio de r unidades, e toda a secção plana perpendicular a um diâmetro fixo da base é um quadrado cuja diagonal é uma corda do círculo. Ach