Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 2

Se R = 0,4 × [ - 1,2 ] , use a soma de Riemann com m = 2 , n = 3 para estimar o valor de

∬ R ( 1 - x y 2 ) d A

Tome os pontos de amostragem como

(a) os cantos inferiores direitos e

(b) como os cantos superiores esquerdos dos retângulos.

Passo 1

Vamos lá pessoal, temos que calcular uma estimativa para uma função utilizando a soma de Riemann, que é da seguinte forma:

∑ i = 1 m ∑ j = 1 n f x * , y * Δ A

Veja que iremos somar os valores da função para alguns valores de x e y , e esses valores de x e y vão depender de quais cantos dos retângulos vamos escolher. Então nossa solução será da seguinte forma:

  1. Vamos construir uma região R para os intervalos dados.
  2. Iremos subdividir essa região na quantidade de espaços especificadas no enunciado.
  3. Iremos calcular o valor da função nos pontos dos cantos conforme solicitado e realizar o somatório de cada retângulo.

Passo 2

  1. Vamos tomar os pontos de amostragem dos cantos inferiores direito.

    2. R e os pontos que serão usados na função. Temos que o intervalo de x é entre 0 ≤ x ≤ 4 e está dividido em m = 2 espaços. Já em y temos o intervalo de - 1 ≤ y ≤ 2 e está dividido em n = 3 . O gráfico desses pontos é:

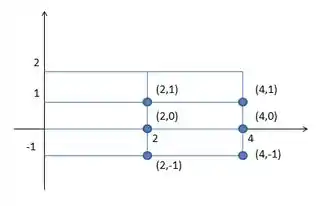
    Considerando os cantos inferiores direitos os pontos são:

    2 , - 1 ; 2,0 ; 2,1 ; 4 , - 1 ; 4,0 ; ( 4,1 )

    E o valor de Δ A ? É a área de cada um dos retângulos. Cada um deles tem base 2 e altura 1 :

    Δ A = 2.1 = 2

    Agora vamos estimar o valor de ∬ R x e - x y d A . Usando a fórmula de Riemann:

    ∬ R 1 - x y 2 d A ≈ ∑ i = 1 2 ∑ j = 1 3 f x , y Δ A

    f x 1 , y 1 Δ A + f x 1 , y 2 Δ A + + f x 1 , y 3 Δ A + f x 2 , y 1 Δ A + f x 2 , y 2 Δ A + f x 2 , y 3 Δ A

    Repare que os pontos x n , y n se referem aos cantos inferiores direitos dos retângulos. Ou seja:

    f 2 , - 1 Δ A + f 2,0 Δ A + + f 2,1 Δ A + f 4,0 Δ A + f 4 , - 1 Δ A + f 4,1 Δ A

    E agora vamos aplicar na função f x , y = 1 - x y 2 os pontos das funções:

    ∬ R 1 - x y 2 d A

    ≈ 2 [ 1 - 2 . - 1 2 + 1 - 2 . 0 2 + 1 - 2 . 1 2

    +   1 - 4 . - 1 2 + 1 - 4 . 0 2 + 1 - 4 . 1 2 ]

    Executando as operações:

    ∬ R ( 1 - x y 2 ) d A = 2 . - 6 = - 12

    Passo 3

  2. Vamos repetir o procedimento para os cantos superiores esquerdos dos retângulos.

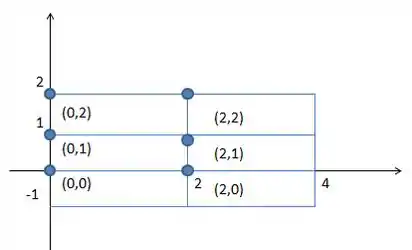O desenho desses pontos é:

Considerando os cantos superiores esquerdos os pontos são:

0,0 ; 0,1 ; 0,2 ; 2,2 ; 2,1 ; ( 2,0 )

O valor de Δ A é o mesmo e vale 2 . Agora é só aplicar a fórmula:

∬ R 1 - x y 2 d A   ≈

f x 1 , y 1 Δ A + f x 1 , y 2 Δ A + + f x 1 , y 3 Δ A + f x 2 , y 1 Δ A + f x 2 , y 2 Δ A + f x 2 , y 3 Δ A

Repare que os pontos x n , y n se referem aos cantos inferiores esquerdos dos retângulos. Ou seja:

f 0,0 Δ A + f 0,1 Δ A + + f 0,2 Δ A + f 2,2 Δ A + f 2,1 Δ A + f 2,0 Δ A

E agora vamos aplicar na função f x , y = 1 - x y 2 nos pontos das funções:

∬ R 1 - x y 2 d A

≈ 2 [ 1 - 2 . 1 2 + 1 - 2 . 0 2 + 1 - 2 . 2 2 +

1 - 0 . 1 2 + 1 - 0 . 2 2 + 1 - 0 . 0 2 ]

Executando as operações:

∬ R ( 1 - x y 2 ) d A = 2 . - 4 = - 8

Resposta

a ) - 12

b ) - 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre int_0^2 f (x , y) d x e int_0^3 f (x , y) d y :f (x , y) = x + 3 x^2 y^2
Calcule a integral iterada.int_0^(pi // 6) int_0^(pi // 2) ( s e n x + s e n y ) d y d x
Calcule a integral iterada.15. ∫ 1 4 ∫ 0 2 6 x 2 y + 2 x d y d x
Calcule a integral iterada. ∫ 0 1 ∫ 0 1 v u + v 2 4d u d v
Encontre int_0^2 f (x , y) d x e int_0^3 f (x , y) d y :f (x , y) = y sqrt(x + 2)