Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 47
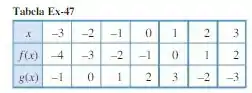
Use a tabela abaixo para fazer um gráfico de .
Passo 1
Para fazer uma gráfico de precisamos saber que funções são essas, certo? Para, depois, achar a composição delas.
Para achar que funções são essas, vamos jogar esses pontos que foram dados na tabela em um gráfico e ver o que aparece.
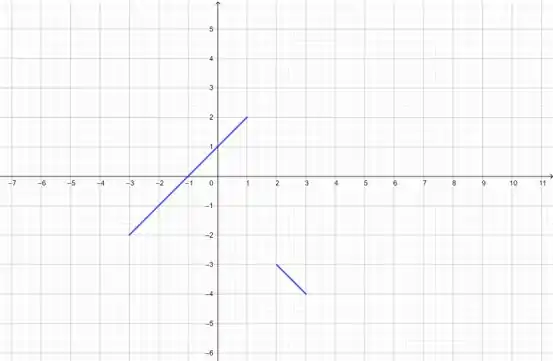
Primeiro, jogando os pontos de :
Opa, a disposição desses pontos parece muuuito com uma reta! Se a gente liga eles, vamos realmente ter uma reta. Mas qual?
Para isso, vamos pegar apenas dois pontos e aplicar na equação da reta:
Para achar os coeficientes e termos a reta correspondente a esses pontos!
Passo 2
Vamos pegar os pontos D e E: e , ok? Substituindo eles na equação da reta:
Daqui, a gente já tira que:
E, no outro ponto:
Substituindo :
Dessa forma, podemos substituir esses valores na equação da reta e:
Vamos ver se ela dá conta dos nossos pontos? Plotando essa reta:
Deu certinho!! Então, !
Passo 3
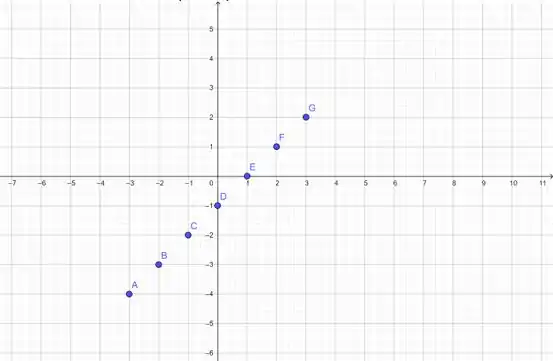
Vamos fazer o mesmo para achar ! Enão, vamos jogar os pontos no gráfico:
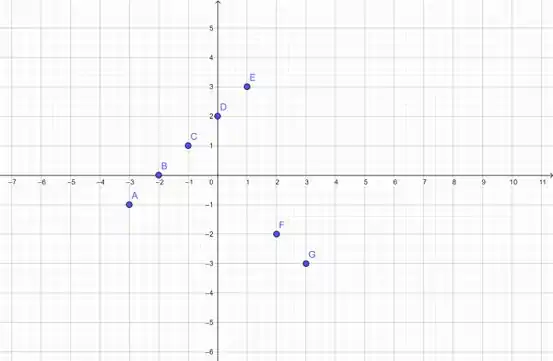
Opa, estranha, essa função né? Mas repare que até o ponto E, temos uma reta e, depois, temos outra. Isso me parece uma função por partes, hein... Vamos achar essas duas retas, então:
Primeiro, a reta de A até E: vamos pegar os pontos D () e E () e jogar na equação da reta:
Ponto D:
Daqui, tiramos que:
E, no ponto E:
Substituindo :
Com isso, temos que de A até E, tem o comportamento de:
Passo 4
Agora, vamos ver os pontos F () e G (). Jogando F na equação da reta:
E G:
Vamos resolver esse sisteminha:
Multiplicando a segunda equação por :
Somando as duas equações:
Substituindo esse valor na primeira equação:
Com isso, de F até G, temos esse comportamento:
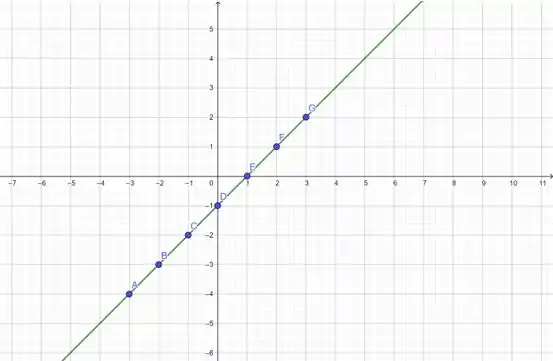
Ok! Juntando as duas informações dos últimos passos, temos que:
Jogando no gráfico:
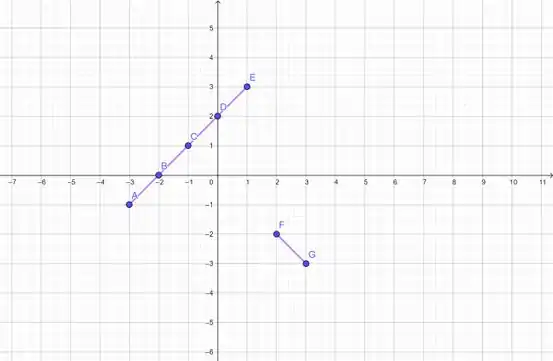
Deu certinho também!
Passo 5
Agora, só falta achar a composição , para isso, precisamos substituir de pela função . Então, como é dada por partes, essas substituições também serão por partes:
Para , . Substituindo em :
Para , . Substituindo em :
Juntando essas informações, podemos definir a composição como:
Vamos jogar isso em um gráfico:
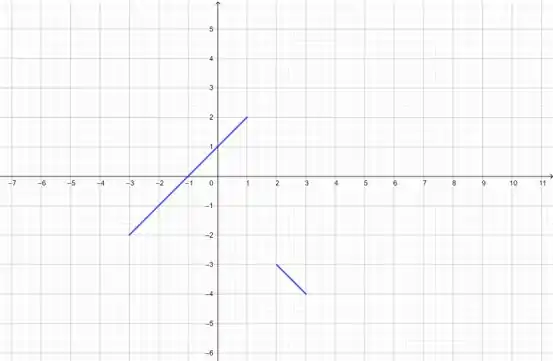
Prontinho!
Resposta
