Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.8 - Ex. 18
Utilize as coordenadas esféricas.
Calcule , onde é a região hemisférica que está acima do plano e abaixo da esfera .
Passo 1
Fala, amigos! Tudo certo?
A questão pede para calcularmos
Onde é a bola unitária é a região hemisférica que está acima do plano e abaixo da esfera
Uma região hemisférica corresponde a metade de uma esfera.
E pede para utilizarmos coordenadas esféricas. Bom, nosso procedimento aqui é parecido com o que a gente vem fazendo. Precisamos dos limites de integração de expressos em coordenadas esféricas e daí podemos partir para o cálculo iterado da nossa integral tripla, começando pela integral “de dentro” até calcular todas as 3 integrais.
A conversão de coordenadas retangulares em esféricas é dada por:
E:
E a distância de um ponto qualquer nesse sistema é dada por:
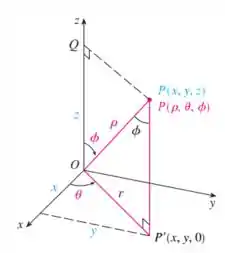
Sistema de coordenadas esféricas
Então, definimos nossa integral em coordenadas esféricas e aí é só partir pro cálculo!
Vamo lá!
Passo 2
Em relação aos limites em coordenadas esféricas que descrevem uma esfera de raio 1 e centrada na origem. Sendo assim, os limites são:
- Raio
- :
- :
Como é uma esfera de raio 1 centrada na origem, teremos:
O ângulo é tomado a partir do eixo . Como estamos olhando somente para a metade da esfera, vamos ter percorrendo somente metade desse ângulo em .
Como no plano temos uma circunferência completa, nosso ângulo varia em:
Com isto, nossa integral se transformará em:
Simplificando:
Pronto, esta é a nossa integral descrita em coordenadas esféricas.
Passo 3
Agora podemos finalmente calcular nossa integral:
Integrando em e tratando como constante, temos:
Aplicando os limites de integração:
Rearranjando os termos e usando a identidade:
Substituindo:
Integrando em e aplicando os limites de integração:
Agora finalmente integramos em :
E esta é a nossa resposta!