Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.8 - Ex. 21

Utilize coordenadas esféricas.

Calcule ∭ E x 2 d V , onde E é limitado pelo plano x z e pelos hemisférios y = 9 - x 2 - z 2 e y = 16 - x 2 - z 2 .

Passo 1

Fala, galerinha! Tudo bom?

A questão quer o valor da integral:

∭ E x 2 d V

onde E está limitado pelos hemisférios:

y = 9 - x 2 - z 2

e

y = 16 - x 2 - z 2

E pelo plano x z .

Bom, vemos que o que falta na nossa integral são os limites de integração da região E . Então de acordo com a descrição da região E dada no enunciado nós vamos achar nossos limites de integração usando coordenadas esféricas, cuja a relação com coordenadas retangulares é:

x = ρ   s e n ϕ cos ⁡ θ

y = ρ   s e n ϕ sen ⁡ θ

z = ρ cos ⁡ ϕ

E:

d V = ρ 2   s e n ϕ   d ρ   d ϕ   d θ  

Também usamos a equação:

ρ 2 = x 2 + y 2 + z 2

Vem!

Passo 2

Podemos começar escrevendo nossa função em coordenadas esféricas.

∭ E x 2 d V

Como:

x = ρ   s e n ϕ cos ⁡ θ

Teremos:

∭ E ρ   s e n ϕ cos ⁡ θ 2   d V

Elevando cada termos ao quadrado:

∭ E ρ 2 sen 2 ⁡ ϕ cos 2 ⁡ θ   d V

Então vamos encontrar os limites de integração da nossa região E .

Passo 3

Vamos entender nossa região E . Sabemos que ela está limitada por dois hemisférios:

y = 9 - x 2 - z 2

e

y = 16 - x 2 - z 2

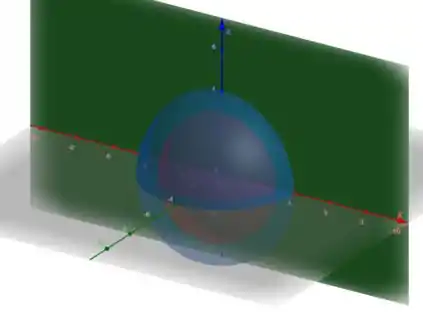
Aqui temos o plano x z (em verde) limitando as duas metades de esferas

Lembrando que um hemisfério é a metade de uma esfera. Bom, vamos reescrever esses hemisférios em coordenadas esféricas. Vamos elevar todas as equações ao quadrado:

y 2 = 9 - x 2 - z 2

e

y 2 = 16 - x 2 - z 2

Isolando as variáveis:

x 2 + z 2 + y 2 = 9

e

x 2 + z 2 + y 2 = 16

Mas lembra que para coordenadas esférica, temos:

ρ 2 = x 2 + y 2 + z 2

Então, teremos:

ρ 2 = 9

e

ρ 2 = 16

Aplicando a raiz quadrada na equação para isolar ρ :

ρ = 3

e

ρ = 4

Como nosso sólido está contido entre esses dois hemisférios, podemos dizer que:

3 ≤ ρ ≤ 4

Passo 4

Pra θ , precisamos olhar no plano x y qual a variação de θ . Olhando nossa imagem no passo anterior, vemos que os hemisférios só ocupam metade do plano x y , então:

0 ≤ θ ≤ π

Por último, nosso ângulo ϕ que parte do eixo z até nosso sólido. Como o sólido começa na parte positiva de z e termina na negativa, significa que ele percorreu meia circunferência:

0 ≤ ϕ ≤ π

Pronto, agora é só substituir. Fazendo:

d V = ρ 2   s e n ϕ   d ρ   d ϕ   d θ  

Ficamos com:

∭ E x 2 d V = ∫ 0 π ∫ 0 π ∫ 3 4 ρ 2 sen 2 ⁡ ϕ cos 2 ⁡ θ ρ 2 sen ⁡ ϕ d ρ d θ d ϕ

Passo 5

Agora que já temos nossa integral em coordenadas esféricas, é só a gente partir pra resolução!

∫ 0 π ∫ 0 π ∫ 3 4 ρ 2 sen 2 ⁡ ϕ cos 2 ⁡ θ ρ 2 sen ⁡ ϕ d ρ d θ d ϕ

Como temos um produto de funções dentro da integral, podemos separar num produto de integrais, cada qual com sua variável.

∫ 0 π cos 2 ⁡ θ d θ ∫ 0 π sen 2 ⁡ ϕ  sen ⁡ ϕ d ϕ ∫ 3 4 ρ 4 d ρ = ∫ 0 π cos 2 ⁡ θ d θ ∫ 0 π sen 3 ⁡ ϕ d ϕ ∫ 3 4 ρ 4   d ρ

Vamos focar em calcular as integrais:

∫ 0 π cos 2 ⁡ θ d θ = ∫ 0 π cos ⁡ 2 θ + 1 2 d θ

Integrando e aplicando os limites de integração:

= 1 2 1 2 sen ⁡ 2 θ + θ 0 π = π 2

Para a outra:

∫ 0 π sen 3 ⁡ θ d θ = ∫ 0 π sen 2 ⁡ θ sen ⁡ θ d θ = ∫ 0 π 1 - cos 2 ⁡ θ sen ⁡ θ   d θ

Fazendo a substituição cos ⁡ θ = z , temos:

∫ 0 π sen 3 ⁡ θ = ∫ 1 - 1 1 - z 2   - d z

Podemos ajustar o sinal e reescrever os limites de integração:

= ∫ - 1 1 1 - z 2   d z

Integrando e aplicando os limites de integração:

= z - 1 3 z 3 - 1 1 = 4 3

Por fim:

∫ 3 4 ρ 4   d ρ = ρ 5 5 3 4 = 781 5

Finalmente, nossa resposta será:

∭ E x 2 d V = π 2 ⋅ 4 3 ⋅ 781 5 = 1562 π 15

Resposta

∭ E x 2 d V = 1562 π 15

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular ∭ T d V , onde T é a casca esférica delimitada por x 2 + y 2 + z 2 = 9 e x 2 + y 2 + z 2 = 16
Calcular ∭_T^() d V , onde T é a região delimitada por x^2 + y^2 + z^2 = a^2 , z = 0 e z= (sqrt(3))/(3) a .
Calcular ∭_T^() ( x^2 + y^2 + z^2 ) . d V , onde T é a esfera x^2 + y^2 + z^2 = 9 e exterior ao cone z^2 = x^2 + y^2
Calcular ∭_T^() ( x ) . d V , onde T é a região limitada por x^2 + ( y - 3 )^2 + ( z - 3 )^2 = 9 .
Calcular as seguintes integrais:int_(- 1)^1 int_0^(sqrt(1 - x^2)) int_0^(sqrt(1 - x^2 - y^2)) ( e^(x^2 + y^2 + z^2) ) d z . d y . d x