Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.4 - Ex. 24
Utilize coordenadas polares para determinar o volume do sólido dado.
Limitado pelo paraboloide e pelo plano no primeiro octante
Passo 1
Beleza, galera?
A questão pede pra gente utilizar coordenadas polares e determinar o volume de um sólido limitado pelo paraboloide
E pelo plano, no primeiro octante,
Jogando essas informações no software, teremos
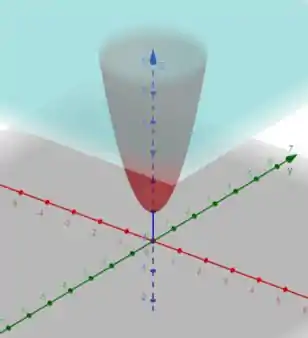
Primeiro precisamos descobrir os limites de integração para calcular uma integral dupla, show?
Relembrando que, em regiões polares, temos essas informações:
Passo 2
Pra descobrir quais vão ser os limites de integração em da integral que representa o volume, vamos igualar os valores de das duas superfícies dadas pelo enunciado:
Então teremos
Como o sólido está no primeiro octante, também teremos
Para esses valores, teremos que
Então a função a ser integrada será:
Logo, nossa integral vai ficar assim:
Passo 3
Podemos separar a integral no produto de duas integrais simples, cada termo com seu integrando:
Resolvendo cada uma, chegaremos a
Substituindo pelos limites de Integración...